题目内容
12.解方程:(1)x+3-x(x+3)=0.
(2)$\frac{x-2}{x+2}$-$\frac{x+2}{x-2}$=$\frac{16}{{{x^2}-4}}$.
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)方程两边都乘以(x+2)(x-2),解整式方程,求出方程的解,最后进行检验即可.
解答 解:(1)分解因式得:(x+3)(1-x)=0,
x+3=0,1-x=0,
x1=-3,x2=1;
(2)方程两边都乘以(x+2)(x-2)得:(x-2)2-(x+2)2=16,
解得:x=-2,
检验:∵当x=-2时,(x+2)(x-2)=0,
∴x=-2是原方程的增根,
所以原方程无解.
点评 本题考查了解一元二次方程和解分式方程,能把一元二次方程转化成一元一次方程是解(1)的关键,能把分式方程转化成整式方程是解(2)的关键.

练习册系列答案
相关题目
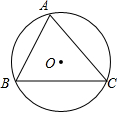 如图,半径为$\sqrt{2}$的⊙O内接△ABC,∠B=60°,∠C=45°
如图,半径为$\sqrt{2}$的⊙O内接△ABC,∠B=60°,∠C=45°
 如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.