题目内容
14.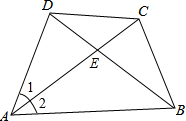 四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
分析 先证明△ABC∽△ADC,得出面积比等于相似比的平方:$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{B{C}^{2}}{C{D}^{2}}$,再由三角形的面积关系求出$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{BE}{DE}$,即可得出结论.
解答 证明:∵AC为AB、AD的比例中项,
∴AC2=AB•AD,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∵AC平分∠DAB,
∴∠1=∠2,
∴△ABC∽△ADC,
∴$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{B{C}^{2}}{C{D}^{2}}$,
∵$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{{S}_{△BCE}}{{S}_{△CDE}}$=$\frac{BE}{DE}$,
∴$\frac{{S}_{△ABE}+{S}_{△BCE}}{{S}_{△ADE}+{S}_{△CDE}}$=$\frac{BE}{DE}$,
∴$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{BE}{DE}$,
∴$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
点评 本题考查了相似三角形的判定与性质、三角形面积的计算、角平分线的定义;熟练掌握相似三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
19.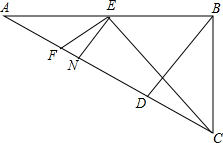 如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
 如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
6.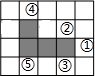 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |

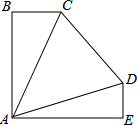 将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.
将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.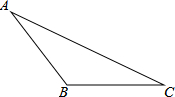 如图,在△ABC中画出高线AD、中线BE、角平分线CF.
如图,在△ABC中画出高线AD、中线BE、角平分线CF.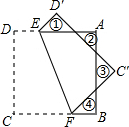 如图,将正方形纸片ABCD沿直线EF折叠,若图中①、②、③、④四个三角形的周长之和为8,则正方形ABCD的面积为4.
如图,将正方形纸片ABCD沿直线EF折叠,若图中①、②、③、④四个三角形的周长之和为8,则正方形ABCD的面积为4.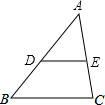 如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE$\stackrel{∥}{=}$$\frac{1}{2}$BC.
如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE$\stackrel{∥}{=}$$\frac{1}{2}$BC.