Question

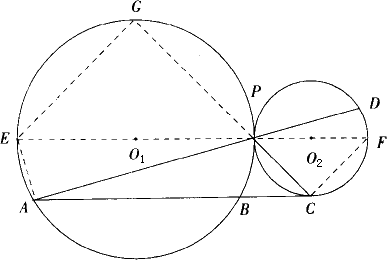
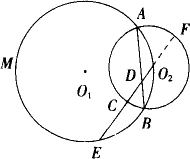
已知如下图，⊙O₁与⊙O₂相交于A、B两点，⊙O₁经过点O₂，E是⊙O₁优弧上的一点，O₂E交⊙O₂于C，交AB于D，又知CD＝1，CE＝2，求O₂E∶O₂D．

Answer 1

答案：
解析：

解：延长CO2交⊙O2于F． 　　∵AB、O2E是⊙O1的两条相交弦， 　　∴O2D·DE＝AD·DB， 　　∵AB、CF是⊙O2的两条相交弦， 　　∴AD·DB＝DC·DF， 　　∴O2D·DE＝DC·DF． 　　设O2D＝x． 　　∵CD＝1，CE＝2， 　　∴DE＝3，DF＝O2D＋O2F＝O2D＋O2C＝2x＋1， 　　∴x×3＝1×(2x＋1)， 　　解得x＝1． 　　∴O2D＝1，O2E＝O2D＋DE＝1＋3＝4． 　　∴O2E∶O2D＝4∶1． 　　分析：观察已知和所求结论，关键是求出O2D的长．一般是作辅助线构造相似三角形来解决，若注意到AB和O2E是⊙O1的两条相交弦，AB和O2C所在的直径是⊙O2的两条相交弦，应用相交弦定理进行解决，解法简洁、明快．