Question

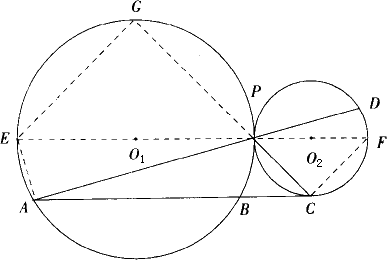
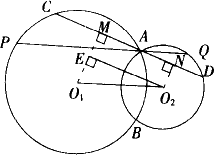
如下图，已知⊙O₁与⊙O₂相交于A、B两点，圆心距为d，过交点A作直线，求直线割两圆所得线段的最大值．

Answer 1

答案：
解析：

解析：假设CD是过点A割两圆所得的线段，作O1M⊥CD于M，O2N⊥CD于N，由垂径定理知，CD＝2MN． 作O2E⊥O1M于点E．要使CD最大，必须MN(即O2E)最大，而O2E的极端(最大)位置是O1O2，所以过点A作O1O2的平行线交⊙O1于P，交⊙O2于Q，线段PQ就是所求的最大线段，PQ＝2d． 　　所以过点A割两圆所得线段的最大值为2d． 　　简评：取Rt△直角边O2E的极端O1O2(斜边)，使得过点A割两圆的最大段得以确定．