Question

如下图所示，已知⊙O₁与⊙O₂相切(包括内切和外切)于点T，求证切点T一定在连心线O₁O₂上．

Answer 1

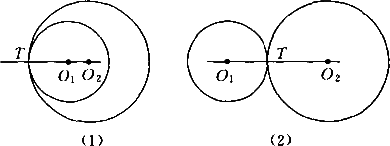
答案：
解析：

证明：假设切点T不在O1O2上， 　　∵连心线O1O2是由⊙O1，⊙O2组成的图形的对称轴， 　　∴点T关于O1O2的对称点也不在O1O2上， 　　并且也是⊙O1和⊙O2的公共点， 　　即⊙O1，⊙O2有两个公共点T，． 　　这与已知⊙O1，⊙O2相切(只有惟一公共点)矛盾． 　　∴⊙O1，⊙O2相切时，切点T在连心线O1O2上． 　　说明：(1)要正确区分连心线和圆心距．连心线是指通过不同心的两个圆圆心的一条直线，而圆心距是指两个圆圆心之间的线段的长度，显然两个圆圆心的连线(线段)一定在连心线(直线)上． 　　(2)“相切两圆的连心线经过切点”也可理解为“相切两圆的圆心、切点在同一条直线上”或“经过相切两圆的切点和一个圆圆心的直线必经过另一个圆的圆心”． 　　(3)两圆相切时，连心线是常见的一条辅助线，使用连心线时，要注意连心线是直线而不是线段，有时也用圆心距．