题目内容
13.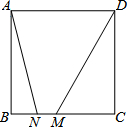 如图,在正方ABCD中,AB=6,MN是BC边上的动线段,且MN=1,则四边形AMND周长的最小值为20.
如图,在正方ABCD中,AB=6,MN是BC边上的动线段,且MN=1,则四边形AMND周长的最小值为20.
分析 在AD上截取AE=1,作EF⊥BC于点G,则DE的长就是AN+DM的最小值,利用三角函数求得DF的长,则四边形周长的最小值即可求得.
解答  解:在AD上截取AE=1,作EF⊥BC于点G.
解:在AD上截取AE=1,作EF⊥BC于点G.
则DE的长就是AN+DM的最小值,
则在直角△DEF中,DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=$\sqrt{(6-1)^{2}+1{2}^{2}}$=13.
则四边形AMND的周长的最小值是13+6+1=20.
故答案是:20.
点评 本题考查了轴对称,以及路径最短问题,正确作出辅助线,确定AN+DM的最小值是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3.已知青椒每斤3元,西红柿每斤2元,小张妈妈以每斤2.5元混合买了a斤青椒和b斤西红柿,结果小张发现妈妈亏钱了,原因是( )
| A. | a<b | B. | a>b | C. | a=b | D. | 与a,b大小无关 |
18.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 正五角星 | D. | 正六边形 |
3.下列说法正确的是( )
| A. | -$\frac{5}{3}$的倒数是$\frac{5}{3}$ | B. | -$\frac{2{x}^{2}y}{3}$的系数是$\frac{2}{3}$ | ||
| C. | -32的值是9 | D. | 3n-4m2n是三次二项式 |
 作图题(要求尺规作图,保留作图痕迹,不写作法)
作图题(要求尺规作图,保留作图痕迹,不写作法)
 某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量x(GB)的之间的函数关系.
某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量x(GB)的之间的函数关系.