题目内容
20.下列命题的逆命题是真命题的是( )| A. | 若a=b,则|a|=|b| | B. | 同旁内角互补 | ||
| C. | 若a+c=b+d,则a=b,c=d | D. | 全等三角形的对应角相等 |
分析 交换原命题的题设与结论得到四个命题的逆命题,然后分别根据绝对值的意义、同旁内角的定义、等式的性质和三角形全等的判定方法判断四个逆命题的真假.
解答 解:A、逆命题为若|a|=|b|,则a=b,此逆命题为假命题,所以A选项错误;
B、逆命题为互补的角为同旁内角,此逆命题为假命题,所以B选项错误;
C、逆命题为若a=b,c=d,则a+c=b+d,此逆命题为真命题,所以C选项正确;
D、逆命题为对应角相等的三角形全等,此逆命题为假命题,所以D选项错误.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.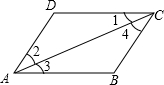 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )
 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )| A. | 因为∠1=∠3,所以AB∥CD(两直线平行,内错角相等) | |
| B. | 因为AB∥CD,所以∠2=∠4(两直线平行,内错角相等) | |
| C. | 因为AD∥BC,所以∠3=∠4(两直线平行,内错角相等) | |
| D. | 因为∠2=∠4,所以AD∥BC(内错角相等,两直线平行) |
9.下列四个命题:①两数之和大于两数之差;②钝角的补角是锐角;③一个数的绝对值总大于这个数本身;④在一个平面内如果直线a⊥直线b,直线b⊥直线c,那么直线a⊥直线c.其中假命题是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
10.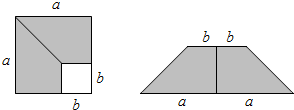 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )| A. | (a-b)2=a2-2ab+b2 | B. | (a+b)2=a2+2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | 无法确定 |
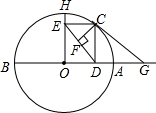 如图,AB是⊙O的直径,AB=6,过点O作OH⊥AB交圆于点H,点C是弧AH上异于A、H的动点,过点C作CD⊥OA,CE⊥OH,垂足分别为D、E,过点C的直线交OA的延长线于点G,且∠GCD=∠CED.
如图,AB是⊙O的直径,AB=6,过点O作OH⊥AB交圆于点H,点C是弧AH上异于A、H的动点,过点C作CD⊥OA,CE⊥OH,垂足分别为D、E,过点C的直线交OA的延长线于点G,且∠GCD=∠CED.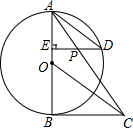 如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:
如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证: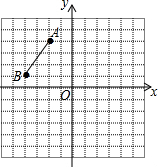 如图,在平面直角坐标系中,A(-2,4),B(-4,1),将线段AB向右平移5个单位、再向下平移1个单位得线段A1B1;将线段A1B1绕原点O旋转180°得线段A2B2,
如图,在平面直角坐标系中,A(-2,4),B(-4,1),将线段AB向右平移5个单位、再向下平移1个单位得线段A1B1;将线段A1B1绕原点O旋转180°得线段A2B2,