题目内容
10．
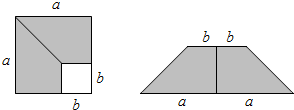如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（ ）| A． | （a-b）2=a2-2ab+b2 | B． | （a+b）2=a2+2ab+b2 | C． | a2-b2=（a+b）（a-b） | D． | 无法确定 |
分析 分别计算这两个图形阴影部分面积，根据面积相等即可得到．
解答 解：第一个图形的阴影部分的面积=a2-b2；
第二个图形是梯形，则面积是$\frac{1}{2}$（2a+2b）•（a-b）=（a+b）（a-b）．
则a2-b2=（a+b）（a-b）．
故选C．
点评 本题考查了平方差公式的几何背景，正确表示出两个图形中阴影部分的面积是关键．
练习册系列答案
阅读快车系列答案
相关题目
20．下列命题的逆命题是真命题的是（ ）
| A． | 若a=b，则|a|=|b| | B． | 同旁内角互补 | ||
| C． | 若a+c=b+d，则a=b，c=d | D． | 全等三角形的对应角相等 |
18．已知x+$\frac{1}{x}$=5，那么x2+$\frac{1}{{x}^{2}}$=（ ）
| A． | 10 | B． | 23 | C． | 25 | D． | 27 |
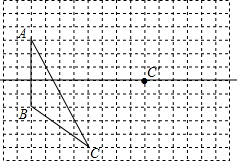画图并填空：如图，方格纸中每个小正方形的边长都为1．
如图：