题目内容
 在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为( )
在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:解直角三角形,正方形的性质,相似三角形的判定与性质
专题:
分析:根据∠NMB=∠MBC,延长MN,BC相交于T,得到等腰△TBM,连接点T和MB的中点,得到相似三角形,然后由相似三角形的性质进行计算,求出∠ABM的正切.
解答: 解:如图:延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,
解:如图:延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,
∵∠ABM+∠MBT=90°,
∠OTB+∠MBT=90°,
∴∠ABM=∠OTB,则△BAM∽△TOB,
∴
=
,即MB2=2AM•BT ①
令DN=1,CT=MD=K,则:AM=2-K,BM=
,BT=2+K,
代入①中得:4+(2-K)2=2(2-K)(2+K),
解方程得:K1=0(舍去),K2=
.
∴AM=2-
=
.
tan∠ABM=
=
=
.
故选A.
 解:如图:延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,
解:如图:延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,∵∠ABM+∠MBT=90°,
∠OTB+∠MBT=90°,
∴∠ABM=∠OTB,则△BAM∽△TOB,
∴
| AM |
| MB |
| OB |
| BT |
令DN=1,CT=MD=K,则:AM=2-K,BM=
| 4+(2-K)2 |
代入①中得:4+(2-K)2=2(2-K)(2+K),
解方程得:K1=0(舍去),K2=
| 4 |
| 3 |
∴AM=2-
| 4 |
| 3 |
| 2 |
| 3 |
tan∠ABM=
| AM |
| AB |
| ||
| 2 |
| 1 |
| 3 |
故选A.
点评:本题考查的是解直角三角形,运用正方形的性质,根据题目中角的关系,判断两个三角形相似,然后用相似三角形的性质进行计算,求出直角三角形中边的长度,再用正切的定义求出角的正切值.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,已知圆周角∠BAD=50°,那么圆周角∠BCD的度数为( )
如图,已知圆周角∠BAD=50°,那么圆周角∠BCD的度数为( )| A、130° | B、100° |
| C、50° | D、40° |
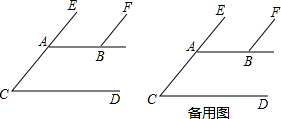
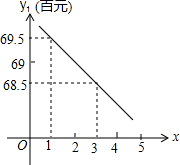 周,房价y2与周数x(6≤x≤12,且x取整数)之间关系如下表:
周,房价y2与周数x(6≤x≤12,且x取整数)之间关系如下表: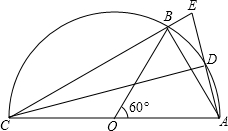 如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.
如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.