题目内容
 抛物线拱桥横截面如图所示,当水面宽4米时,拱顶离水面2米,若水面上升1米,则水面宽度将减少
抛物线拱桥横截面如图所示,当水面宽4米时,拱顶离水面2米,若水面上升1米,则水面宽度将减少考点:二次函数的应用
专题:
分析:设抛物线的解析式为y=ax2,由待定系数法求出二次函数的解析式,再将y=1时求出x的值,就可以求出此时水面的宽度,进而求出结论.
解答:解:设抛物线的解析式为y=ax2,由题意,得
-2=4a,
解得:a=-
,
∴y=-
x2,
当y=-1时,
-1=-
x2,
解得:x=±
,
∴水面宽度减少了(4-2
)米.
故答案为:4-2
.
-2=4a,
解得:a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
当y=-1时,
-1=-
| 1 |
| 2 |
解得:x=±
| 2 |
∴水面宽度减少了(4-2
| 2 |
故答案为:4-2
| 2 |
点评:本题考查了待定系数法求二次函数的解析式的运用,由函数值求自变量的值的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
一件上衣售价为m元,获利10%,则进价为( )
| A、10πm元 | ||
B、
| ||
| C、(1+10%)m元 | ||
D、
|
 如图,在我市初中学业水平考试体育科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线O-B-C-D,下列说法正确的是( )
如图,在我市初中学业水平考试体育科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线O-B-C-D,下列说法正确的是( )| A、小莹的速度随时间的增大而增大 |
| B、小梅的平均速度比小莹的平均速度大 |
| C、在起跑后86.4秒时,两人相遇 |
| D、在起跑后50秒内,小梅比小莹慢 |
2013年东莞市生产总值(GDP)约5490亿元,比上年增长9.8%,5490亿用科学记数法表示为( )
| A、5.49×1010元 |
| B、0.549×1011元 |
| C、54.9×1010元 |
| D、5.49×1011元 |
 如图,在⊙O中,直径AB交弦ED于点G,EG=DG,⊙O的切线BC交DO的延长线于点C,F是DC与⊙O的交点,连结AF.
如图,在⊙O中,直径AB交弦ED于点G,EG=DG,⊙O的切线BC交DO的延长线于点C,F是DC与⊙O的交点,连结AF.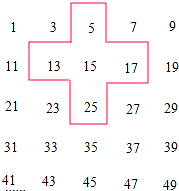 将连续奇数1,3,5,7,9,11,…,排成如下的数表,请回答下列问题:
将连续奇数1,3,5,7,9,11,…,排成如下的数表,请回答下列问题: 等边△ABC在平面直角坐标系内的位置如图所示,已知△ABC的边长为6,则点A的坐标为
等边△ABC在平面直角坐标系内的位置如图所示,已知△ABC的边长为6,则点A的坐标为