题目内容
5.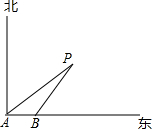 如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)
如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)
分析 过点P作PC⊥AB于C点,在Rt△PAC中,根据三角函数AC、BC就可以PC表示出来,在直角△PAC中,根据三角函数,就得到一个关于PC的方程,求得PC.
解答 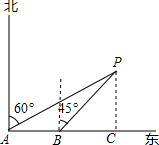 解:过点P作PC⊥AB于C点,即PC的长为轮船与灯塔的最短距离,根据题意,得
解:过点P作PC⊥AB于C点,即PC的长为轮船与灯塔的最短距离,根据题意,得
AB=18×$\frac{20}{60}$=6,∠PAB=90°-60°=30°,∠PBC=90°-45°=45°,∠PCB=90°,
∴PC=BC,
在Rt△PAC中,tan30°=$\frac{PC}{AB+BC}$=$\frac{PC}{6+PC}$,即$\frac{\sqrt{3}}{3}$=$\frac{PC}{6+PC}$,
解得PC=3$\sqrt{3}$+3≈8.2(海里),
∴轮船与灯塔的最短距离约为8.2海里.
点评 本题主要考查解直角三角形在实际问题中的应用,构造直角三角形是解题的前提和关键.

练习册系列答案
相关题目
13.若不等式(-a+1)x>1-a的解集是x<1,则a必满足( )
| A. | a<0 | B. | a>1 | C. | a<-1 | D. | a<1 |
20.2015年央视春晚微信摇一摇互动总量达110亿次,将110亿用科学记数法表示为( )
| A. | 110×108 | B. | 11×109 | C. | 1.1×1010 | D. | 1.1×1011 |
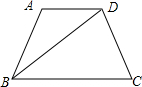 如图,已知在梯形ABCD中,AD∥BC,已知$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{BD}$,那么$\overrightarrow{BD}$=$\overrightarrow{b}$-$\overrightarrow{a}$.
如图,已知在梯形ABCD中,AD∥BC,已知$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{BD}$,那么$\overrightarrow{BD}$=$\overrightarrow{b}$-$\overrightarrow{a}$.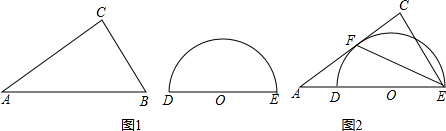
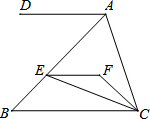 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=130°,∠FEC=15°,求∠ACF的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=130°,∠FEC=15°,求∠ACF的度数.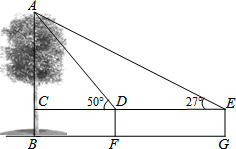 某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)