题目内容
2. 如图,AB是⊙O的直径,C、D在⊙O上,D是弧AC的中点,过点D作DE⊥BC于点E,并交BA延长线于点F,若AB=9,CE=1,则AD的长为( )
如图,AB是⊙O的直径,C、D在⊙O上,D是弧AC的中点,过点D作DE⊥BC于点E,并交BA延长线于点F,若AB=9,CE=1,则AD的长为( )| A. | 2 | B. | 2.4 | C. | 3 | D. | 3.6 |
分析 连接AD,OD、AC,OD交AC于点M,由圆周角定理得出∠ACB=90°,OD=OA=$\frac{1}{2}$AB=4.5,得出∠ECM=90°,由垂径定理得出OD⊥AC,证出四边形DECM是矩形,得出DM=CE=1,∴OM=OD-DM=3.5,在Rt△AOM中,由勾股定理得出AM=2$\sqrt{2}$,在Rt△AOD中,由勾股定理求出AD即可.
解答 解:连接AD,OD、AC,OD交AC于点M,如图所示:
∵AB是⊙O的直径,
∴∠ACB=90°,OD=OA=$\frac{1}{2}$AB=4.5,
∴∠ECM=90°,
∵D是弧AC的中点,
∴OD⊥AC,
∴四边形DECM是矩形,
∴DM=CE=1,
∴OM=OD-DM=3.5,
在Rt△AOM中,AM=$\sqrt{O{A}^{2}-O{M}^{2}}$=$\sqrt{4.{5}^{2}-3.{5}^{2}}$=2$\sqrt{2}$,
在Rt△AOD中,AD=$\sqrt{O{D}^{2}-A{M}^{2}}$=$\sqrt{9}$=3;
故选:C.
点评 本题考查了圆周角定理、垂径定理、矩形的判定与性质、勾股定理;熟练掌握圆周角定理和垂径定理,证出四边形是矩形是解决问题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7.在Rt△ABC中,∠C=90°,a=1,b=$\sqrt{3}$,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( )
| A. | π | B. | 1 | C. | $\frac{2}{3}$π | D. | 2 |
11.合并同类项2a2b-2ab2-a2b,结果正确的是( )
| A. | 0 | B. | -a2b | C. | -1 | D. | a2b-2ab2 |
12.下列说法正确的是( )
| A. | 平方等于它本身的数是0 | B. | 立方等于它本身的数是±1 | ||
| C. | 绝对值等于它本身的数是正数 | D. | 倒数等于它本身的数是±1 |
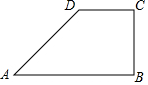 如图,四边形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.
如图,四边形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.