题目内容
18.若两个无理数的和是有理数,则这两个无理数可以是:-$\sqrt{2}$,$\sqrt{2}$.分析 根据互为相反数之和为0解答即可.
解答 解:∵-$\sqrt{2}$+$\sqrt{2}$=0,0是有理数,
∴这两个无理数可以是-$\sqrt{2}$和$\sqrt{2}$,
故答案为:-$\sqrt{2}$;$\sqrt{2}$.
点评 本题考查的是实数的概念以及实数的加减运算,掌握有理数和无理数统称实数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在端午节道来之前,双十中学高中部食堂推荐了A,B,C三家粽子专卖店,对全校师生爱吃哪家店的粽子作调查,以决定最终向哪家店采购.下面的统计量中最值得关注的是( )
| A. | 方差 | B. | 平均数 | C. | 中位数 | D. | 众数 |
8.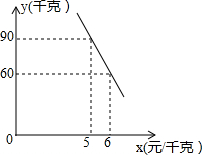 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.(1)根据题意,填写如表:
| 蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
| 所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
 如图,正方形ABCD的两边BC、AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3$\sqrt{2}$,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是$\frac{1}{3}$.
如图,正方形ABCD的两边BC、AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3$\sqrt{2}$,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是$\frac{1}{3}$.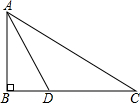 如图所示,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果精确到0.1)
如图所示,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果精确到0.1)
 如图所示,抛物线y=ax2+bx+c(a≠0),过点(-1,0)和点(3,0),则抛物线的顶点横坐标是1.
如图所示,抛物线y=ax2+bx+c(a≠0),过点(-1,0)和点(3,0),则抛物线的顶点横坐标是1.