Question

6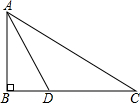．如图所示，某中学九年级数学兴趣小组测量校内旗杆AB的高度，在C点测得旗杆顶端A的仰角∠BCA=30°，向前走了20米到达D点，在D点测得旗杆顶端A的仰角∠BDA=60°，求旗杆AB的高度．（结果精确到0.1）
参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732．

Answer 1

分析 根据题意得∠C=30°，∠ADB=60°，从而得到∠DAC=30°，进而判定AD=CD，得到CD=20米，在Rt△ADB中利用sin∠ADB求得AB的长即可．

解答 解：∵∠C=30°，∠ADB=60°，
∴∠DAC=30°，
∴AD=CD，
∵CD=20米，
∴AD=20米，
在Rt△ADB中，sin∠ADB=$\frac{AB}{AD}$，
则AB=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$≈17.3米，
答：旗杆AB的高度约为17.3米．

点评 此题主要考查了解直角三角形的应用-仰角俯角问题，解题的关键是从题目中整理出直角三角形并正确的利用边角关系求解．