题目内容

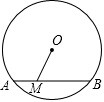如图，⊙O的半径为5，M是
AB
上任意一点，且OM最小值为4，则弦AB=
 
．
考点：垂径定理,勾股定理
专题：
分析：过点O作OD⊥AB于点D，则当M与D重合时最短，AB=2BD，再根据勾股定理求出BD的长即可．
解答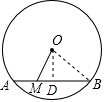：解：过点O作OD⊥AB于点D，则当M与D重合时最短，AB=2BD，
∵OB=5，OD=OM=4，
∴BD=
OB2-OD2
=
52-42
=3，
∴AB=2BD=6．
故答案为：6．
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
作图题：
（1）画出图（1）△ABC关于直线AC对称的△AB′C，再画出△AB′C关于直线B′C对称的△A′B′C．
（2）如图（2），两条公路OA和OB相交于O点，在∠AOB的内部有工厂C和D，现要修建一个货站P，使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹，写出结论）
如图1，△ABC中，CA=CB，点O在高CH上，OD⊥CA于点D，OE⊥CB于点E，以O为圆心，OD为半径作⊙O．
（1）求证：⊙O与CB相切于点E；
（2）如图2，若⊙O 过点H，且AC=5，AB=6，连结EH，求△BHE的面积．
计算 （2-3）-1-（
2
-1）0=
 
，若（a+b）-2有意义，则a与b的关系式
 
．
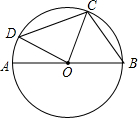如图，已知AB为⊙O直径，∠DOC=90°，∠DOC绕点O旋转，D、C两点不与A、B重合．
（1）求证：
AB
+
BC
=
CD
；
（2）AD+BC=CD成立吗？为什么？
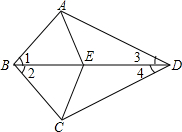已知：如图，∠1=∠2，∠3=∠4，点E在BD上，连结AE、CE，求证：AE=CE．
已知关于x的方程mx+2=x①的根是负实数，（m-2）x2+（2m-3）x-1+m=0②有实根，则m的取值是
 
．
在△ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段上的动点，将线段PA绕点P顺时针旋转2α得到线段PQ．线段CQ的延长线交射线BM于点D，连接AD．

（1）若α=60°且点P与点M重合（如图1），求证四边形ABCD为菱形；
（2）在图2中，点P不与点B，M重合，猜想∠CDB的大小（用含α的代数式表示），并加以证明；
（3）对于适当大小的α，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ=QD，请直接写出α的范围．
把方程（2x+1）（3x-2）=2化为一般形式为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网