题目内容
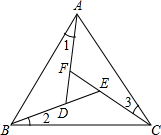
 如图,在四边形ABCD中,已知AD∥BC,∠1=∠2,试说明∠3+∠4=180°.
如图,在四边形ABCD中,已知AD∥BC,∠1=∠2,试说明∠3+∠4=180°.考点:平行线的判定与性质
专题:证明题
分析:由AD∥BC,根据平行线的性质得∠1=∠3,再利用等量代换得∠3=∠2,则根据平行线的判定可得BE∥DF,然后根据平行线的性质有∠3+∠4=180°.
解答:证明:∵AD∥BC,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴BE∥DF,
∴∠3+∠4=180°.
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴BE∥DF,
∴∠3+∠4=180°.
点评:本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知⊙O的半径为10cm,如果圆心O到一条直线的距离为10cm,那么这条直线和这个圆的位置关系为( )
| A、相离 | B、相切 |
| C、相交 | D、无法确定 |
若
=
,则
=( )
| x+y |
| x |
| 5 |
| 3 |
| x-y |
| 2x |
| A、6 | ||
B、
| ||
C、
| ||
| D、不确定 |
下列变形中正确的是( )
| A、由3x-5=2x,得3x+2x=5 | ||
B、由-7x=3,得x=-
| ||
| C、由2(x-4)=4,得2x-1=4 | ||
| D、由-5y=0,得y=0 |
 如图,已知在△ABC中,∠BAC=∠ACB=∠CBA,∠1=∠2=∠3.
如图,已知在△ABC中,∠BAC=∠ACB=∠CBA,∠1=∠2=∠3.