题目内容
已知关于x的一元二次方程x2﹣2mx+m2﹣m=o有两个实数根a、b;
(1)求实数m的取值范围;
(2)求代数式a2+b2﹣3ab的最大值.
【考点】根的判别式;根与系数的关系;配方法的应用.
【分析】(1)根据判别式的意义得到△=(﹣2m)2﹣4(m2﹣m)≥0,然后解不等式即可;
(2)由根与系数的关系得出a+b=2m,ab=m2﹣m,将代数式a2+b2﹣3ab变形为(a+b)2﹣5ab=﹣m2+5m=﹣(m﹣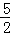 )2+
)2+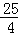 ,即可求出最大值.
,即可求出最大值.
【解答】解:(1)根据题意得△=(﹣2m)2﹣4(m2﹣m)≥0,
解得m≥0;
(2)∵关于x的一元二次方程x2﹣2mx+m2﹣m=0有两个实数根a、b,
∴a+b=2m,ab=m2﹣m,
∴a2+b2﹣3ab=(a+b)2﹣5ab
=(2m)2﹣5(m2﹣m)
=﹣m2+5m
=﹣(m﹣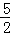 )2+
)2+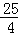 ,
,
由(1)得m≥0,
∴代数式a2+b2﹣3ab的最大值为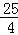 .
.
【点评】本题考查了一元二次方程根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
也考查了根与系数关系,配方法的应用.

练习册系列答案
相关题目

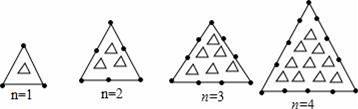




 (x>0) B.y=
(x>0) B.y=
 (x>0) C.y=
(x>0) C.y=