题目内容
 如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,BC′交AD于点E,若AB=4,AD=8,则DE的长为( )
如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,BC′交AD于点E,若AB=4,AD=8,则DE的长为( )| A、2 | B、3 | C、4 | D、5 |
考点:翻折变换(折叠问题)
专题:
分析:首先根据题意得到BE=DE,然后根据勾股定理得到关于线段AB、AE、BE的方程,解方程即可解决问题.
解答: 解:
解:
设ED=x,则AE=8-x;
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴EB=ED=x;
由勾股定理得:
BE2=AB2+AE2,
即x2=42+(8-x)2,
解得:x=5,
故选D.
 解:
解:设ED=x,则AE=8-x;
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴EB=ED=x;
由勾股定理得:
BE2=AB2+AE2,
即x2=42+(8-x)2,
解得:x=5,
故选D.
点评:该命题主要考查了几何变换中的翻折变换及其应用问题;解题的关键是根据翻折变换的性质,结合全等三角形的判定及其性质、勾股定理等几何知识,灵活进行判断、分析、推理或解答.

练习册系列答案
相关题目
下列说法正确的是( )
A、在球的体积公V=
| ||||
| B、若变量x、y满足y2=x,则y是x的函数 | ||||
C、在圆锥的体积公式V=
| ||||
D、若变量x、y满足y=-
|
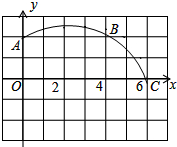 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题: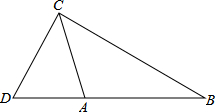 如图,在△ABC中,AC=5cm,BC=8cm,△ABC的面积为12cm,点D在BA延长线上,∠DCA=∠B.
如图,在△ABC中,AC=5cm,BC=8cm,△ABC的面积为12cm,点D在BA延长线上,∠DCA=∠B.