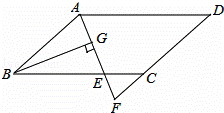
题目内容
如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=
 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )


A.﹣2 B.﹣4 C.﹣
 D.
D.

C【考点】反比例函数图象上点的坐标特征.
【分析】作AD⊥x轴于D,CE⊥x轴于E,先通过证得△AOD≌△OCE得出AD=OE,OD=CE,设A(x,
 ),则C(
),则C(
 ,﹣x),根据正方形的性质求得对角线解得F的坐标,根据直线OB的解析式设出直线AC的解析式为:y=﹣
,﹣x),根据正方形的性质求得对角线解得F的坐标,根据直线OB的解析式设出直线AC的解析式为:y=﹣
 x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
【解答】解:作AD⊥x轴于D,CE⊥x轴于E,
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,

 ,
,
∴△AOD≌△OCE(AAS),
∴AD=OE,OD=CE,
设A(x,
 ),则C(
),则C(
 ,﹣x),
,﹣x),
∵点B的坐标为(1,4),
∴OB=
 =
=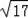
 ,
,
直线OB为:y=4x,
∵AC和OB互相垂直平分,
∴它们的交点F的坐标为(
 ,2),
,2),
设直线AC的解析式为:y=﹣
 x+b,
x+b,
代入(
 ,2)得,2=﹣
,2)得,2=﹣
 ×
×
 +b,解得b=
+b,解得b=
 ,
,
直线AC的解析式为:y=﹣
 x+
x+
 ,
,
把A(x,
 ),C(
),C(
 ,﹣x)代入得
,﹣x)代入得

 ,解得k=﹣
,解得k=﹣
 .
.
故选C.

【点评】本题考查了反比例函数图象上点的坐标特征,待定系数法求解析式,正方形的性质,三角形求得的判定和性质,熟练掌握正方形的性质是解题的关键.

练习册系列答案
相关题目


 的解为
的解为 ,则
,则


 即
即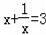
 ,
,




 = 4 ,
= 4 ,
 = 14 ,
= 14 ,
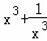

 的解,但不是方程x2﹣3x+2=0的实数解的概率为
的解,但不是方程x2﹣3x+2=0的实数解的概率为 


 求t的值;
求t的值; S△ABC?若存在,请求出t的值;若不存在,请说明理由.
S△ABC?若存在,请求出t的值;若不存在,请说明理由.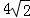 ,则梯形AECD的
,则梯形AECD的