题目内容
19.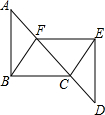 如图,已知A,F,C,D四点在同一条直线上,AF=CD,∠A=∠D,AB=DE,则BC=EF,请说明理由(完成下列填空)
如图,已知A,F,C,D四点在同一条直线上,AF=CD,∠A=∠D,AB=DE,则BC=EF,请说明理由(完成下列填空)解:∵AF=CD(已知)
∴AF+FC=CD+FC
即AC=DF
在△ABC和△DEF中
$\left\{\begin{array}{l}{()}\\{∠A=∠D(已知)}\\{AB=DE()}\end{array}\right.$
∵△ABC≌△DEF( )
∴BC=EF( )
分析 本题考查的是全等三角形的判定(SAS),填空题有一定的提示作用,相对要简单的多.
解答 解:∵AF=CD(已知),
∴AF+FC=CD+FC,即AC=DF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AC=DF(已证)}\\{∠A=∠D(已知)}\\{AB=DE(已知)}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴BC=EF(全等三角形对应边相等).
故答案为:FC;AC;DF.
点评 此题考查全等三角形的判定和性质,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 如图,四边形ABCD边长为a的正方形,点E在CD上,DE=b,AE=c,延长CB至点F,使BF=b,连接AF,试利用此图证明勾股定理.
如图,四边形ABCD边长为a的正方形,点E在CD上,DE=b,AE=c,延长CB至点F,使BF=b,连接AF,试利用此图证明勾股定理. 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过点D作DE⊥MN于点E.
如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过点D作DE⊥MN于点E. 如图,某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.若其中一个控制电灯的开关坏了(不知是哪一个),则任意按下两个开关,正好一盏灯亮和一个吊扇转的概率是$\frac{1}{3}$.
如图,某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.若其中一个控制电灯的开关坏了(不知是哪一个),则任意按下两个开关,正好一盏灯亮和一个吊扇转的概率是$\frac{1}{3}$.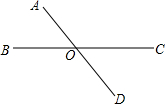 如图,直线AD、BC交于点O,且∠AOB+∠COD=100°,则∠AOC的度数为125°.
如图,直线AD、BC交于点O,且∠AOB+∠COD=100°,则∠AOC的度数为125°.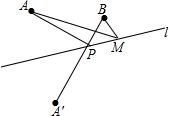 如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.
如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.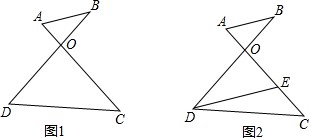 如图,线段AC与BD交于点O,且AO=3,BO=5,AC=18,OD=9.
如图,线段AC与BD交于点O,且AO=3,BO=5,AC=18,OD=9.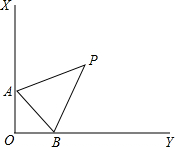 如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.
如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.