题目内容
5．先化简，再求值：（1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4x+4}{x+1}$，其中x=2+$\sqrt{2}$．分析 先根据分式的运算法则化简，再把x的值代入计算即可．
解答 解：
（1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4x+4}{x+1}$
=$\frac{x+1-3}{x+1}$×$\frac{x+1}{（x-2）^{2}}$
=$\frac{x-2}{x+1}$×$\frac{x+1}{（x-2）^{2}}$
=$\frac{1}{x-2}$
∴当x=2+$\sqrt{2}$时，
原式=$\frac{1}{2+\sqrt{2}-2}$=$\frac{\sqrt{2}}{2}$．
点评 本题主要考查分式的计算，掌握分式的运算法则是解题的关键．
练习册系列答案
相关题目
15．
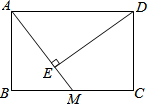如图，在矩形ABCD中，AB=1，BC=$\frac{5}{2}$，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为（ ）
如图，在矩形ABCD中，AB=1，BC=$\frac{5}{2}$，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为（ ）| A． | 1 | B． | $\frac{3\sqrt{13}}{13}$ | C． | $\frac{10\sqrt{41}}{41}$ | D． | $\frac{\sqrt{41}}{10}$ |
16．在实数-3，0，$\sqrt{3}$，3中，最小的实数是（ ）
| A． | -3 | B． | 0 | C． | $\sqrt{3}$ | D． | 3 |
如图所示，在平面直角坐标系中，点C（0，-8），点A、B在x轴上，且CA=CB=10．
15．下列计算正确的是（ ）
| A． | 4$\sqrt{3}$-3$\sqrt{3}$=1 | B． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C． | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | D． | $\sqrt{\frac{1}{3}}$•$\sqrt{27}$=$\frac{\sqrt{3}}{3}$ |