Question

2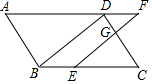．如图，在平行四边形ABCD中，点E在边BC上，过点E作BD的平行线交DC于点G、交AD的延长线于点F．
（1）求证：DF=BE；
（2）若$\frac{DG}{GC}$=$\frac{1}{2}$，BE=2，求BC的长．

Answer 1

分析 （1）由四边形ABCD是平行四边形，得到AF∥BC，由于EF∥BD，推出四边形BDFE是平行四边形，根据平行四边形的性质即可得到结论；
（2）根据相似三角形的性质得到$\frac{DG}{GC}=\frac{DF}{EC}$，即$\frac{1}{2}$=$\frac{2}{EC}$，于是得到结论．

解答 解：（1）∵四边形ABCD是平行四边形，
∴AF∥BC，
∵EF∥BD，
∴四边形BDFE是平行四边形，
∴BE=DF；

（2）∵BE=DF，BE=2，
∴DF=2，
∵AF∥BC，
∴△DGF∽△CGE，
∴$\frac{DG}{GC}=\frac{DF}{EC}$，即$\frac{1}{2}$=$\frac{2}{EC}$，
∴EC=4，
∴BC=BE+EC=2+4=6．

点评 本题考查了相似三角形的判定和性质，平行四边形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．