题目内容
12. 如图,已知数轴上点A表示的数为8,B是数轴上原点左边的一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动.
如图,已知数轴上点A表示的数为8,B是数轴上原点左边的一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动.(1)写出数轴上点B表示的数-6,点P运动t(t>0)秒后表示的数-5t+8(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若P、Q两点同时出发,那么点P运动多少时间后追上点Q?
分析 (1)由点A表示的数结合AB的长度可得出点B表示的数,由点P的运动方向及速度结合点A表示的数,即可找出点P运动t秒后表示的数;
(2)找出运动时间t秒后点Q表示的数,令点P、Q表示的数相等,即可得出关于t的一元一次方程,解之即可得出结论.
解答 解:(1)∵数轴上点A表示的数为8,B是数轴上原点左边的一点,且AB=14,
∴点B表示的数为8-14=-6.
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,
∴点P运动t秒后表示的是为-5t+8.
故答案为:-6;-5t+8.
(2)当运动时间为t秒时,点Q表示的数为-3t-6,点P表示的数为-5t+8,
根据题意得:-3t-6=-5t+8,
解得:t=7.
答:若P、Q两点同时出发,点P运动7秒后追上点Q.
点评 本题考查了一元一次方程的应用以及数轴,解题的关键是:(1)由点P的运动方向及速度结合点A表示的数,找出点P运动t秒后表示的数;(2)令点P、Q表示的数相等,列出关于t的一元一次方程.

练习册系列答案
相关题目
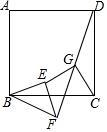 已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由.
已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由. 已知:如图,等边△ABC中,D为BC上一点.CE为△ABC的外角角平分线,连接DE,若DE=DA,求证:△ADE为等边三角形.
已知:如图,等边△ABC中,D为BC上一点.CE为△ABC的外角角平分线,连接DE,若DE=DA,求证:△ADE为等边三角形.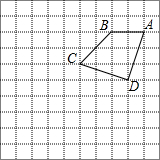 如图,在正方形网格图中,点A、B、C、D均在格点上,以点A为位似中心,将四边形ABCD放大到原来的2倍得到四边形AB′C′D′.
如图,在正方形网格图中,点A、B、C、D均在格点上,以点A为位似中心,将四边形ABCD放大到原来的2倍得到四边形AB′C′D′.