Question

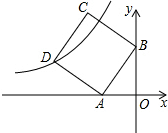如图，在平面直角坐标系中，直线y=2x+4与x轴、y轴分别交于A、B两点，以AB为边在第二象限作正方形ABCD，点D在双曲线y=

k

x

(x＜0)上，将正方形ABCD沿x轴正方向平移a个单位长度后，点C恰好也落在此双曲线上，则a的值是

 

．

Answer 1

考点：反比例函数综合题

专题：

分析：作CE⊥y轴于点E，交双曲线于点G．作DF⊥x轴于点F，易证△OAB≌△FDA≌△BEC，求得A、B的坐标，根据全等三角形的性质可以求得C、D的坐标，从而利用待定系数法求得反比例函数的解析式，进而求得G的坐标，则a的值即可求解．

解答：解：过点CE⊥y轴于点E，交双曲线于点G，过点D作DF⊥x轴于点F，
在y=2x+4中，令x=0，解得：y=4，即B的坐标是（0，4）．
令y=0，解得：x=-2，即A的坐标是（-2，0）．
则OB=4，OA=2．
∵∠BAD=90°，
∴∠BAO+∠DAF=90°，
又∵直角△ABO中，∠BAO+∠OBA=90°，
∴∠DAF=∠OBA，
在△OAB和△FDA中，

∠DAF=∠OBA  ∠BOA=∠AFD  AB=AD

，
∴△OAB≌△FDA（AAS），
同理，△OAB≌△FDA≌△BEC，
∴AF=OB=EC=4，DF=OA=BE=2，
∴D的坐标是（-6，2），C的坐标是（-4，6）．
将点D代入y=

k

x

得：k=-12，则函数的解析式是：y=-

12

x

．
∴OE=6，
则C的纵坐标是6，把y=6代入y=-

12

x

得：x=-2．
即G的坐标是（-2，6），
∴CG=4-2=2．
∴a=2．
故答案为：2．

点评：本题考查了正方形的性质，全等三角形的判定与性质以及待定系数法求函数的解析式等知识．此题综合性较强，难度适中，注意正确求得C、D的坐标是关键，注意掌握数形结合思想与方程思想的应用．