题目内容
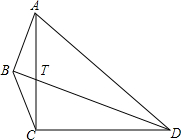 在四边形ABCD中,AC⊥CD,AC=CD,∠ABD=90°,BD平分∠APC,交AC于点T.求证:DT=2AB.
在四边形ABCD中,AC⊥CD,AC=CD,∠ABD=90°,BD平分∠APC,交AC于点T.求证:DT=2AB.考点:全等三角形的判定与性质
专题:证明题
分析:延长DC和AB,它们相交于E,如图,先利用等角的余角相等得到∠BAT=∠CDT,则可根据“AAS”判断△ACE=≌△DCT,则AE=DT,由于BD平分∠APC,BD⊥AE,根据等腰三角形的性质得AB=EB,于是有DT=2AB.
解答: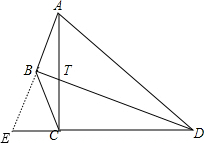 解:延长DC和AB,它们相交于E,如图,
解:延长DC和AB,它们相交于E,如图,
∵AC⊥CD,
∴∠ACE=90°,
∵∠ABD=90°,∠ATB=CTD,
∴∠BAT=∠CDT,
在△ACE和△DCT中,
,
∴△ACE=≌△DCT(AAS),
∴AE=DT,
∵BD平分∠APC,BD⊥AE,
∴AB=EB,
∴AE=2AB,
∴DT=2AB.
 解:延长DC和AB,它们相交于E,如图,
解:延长DC和AB,它们相交于E,如图,∵AC⊥CD,
∴∠ACE=90°,
∵∠ABD=90°,∠ATB=CTD,
∴∠BAT=∠CDT,
在△ACE和△DCT中,
|
∴△ACE=≌△DCT(AAS),
∴AE=DT,
∵BD平分∠APC,BD⊥AE,
∴AB=EB,
∴AE=2AB,
∴DT=2AB.
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.灵活运用等腰三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
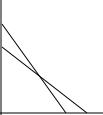 如图,一架长为10m的梯子斜靠在一面墙上,梯子底端离墙6m,如果梯子的顶端下滑了2m,那么梯子底部在水平方向滑动了( )
如图,一架长为10m的梯子斜靠在一面墙上,梯子底端离墙6m,如果梯子的顶端下滑了2m,那么梯子底部在水平方向滑动了( )| A、2m | B、2.5m |
| C、3m | D、3.5m |
 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
若A、O、B三点在同一条直线上,OA=3,OB=5,则A、B两点间的距离为( )
| A、2 | B、8 | C、3 | D、8或2 |
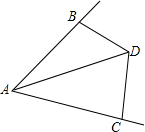 如图,已知AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD.
如图,已知AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD. 如图,A,B,C三点在同一直线上,使得AB=4,BC=3,如果点O是线段AC的中点,则线段OB的长度为
如图,A,B,C三点在同一直线上,使得AB=4,BC=3,如果点O是线段AC的中点,则线段OB的长度为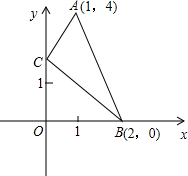 在平面直角坐标系中,已知两点A(1,4)B(2,0),点C是y轴上的一个动点,且A、B、C三点不共线,求△ABC周长的最小值及相应点C的坐标.
在平面直角坐标系中,已知两点A(1,4)B(2,0),点C是y轴上的一个动点,且A、B、C三点不共线,求△ABC周长的最小值及相应点C的坐标.