题目内容
 如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC
如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线.
(1)写出图中与∠EOC互余的角;
(2)求∠AOE的度数.
考点:余角和补角
专题:
分析:(1)先求出∠AOC度数,根据角平分线定义求出∠AOE、∠EOC、∠BOD、∠COD,根据互余的定义判断即可;
(2)根据角平分线定义和∠AOC的度数得出即可.
(2)根据角平分线定义和∠AOC的度数得出即可.
解答:解:(1)∵点O是直线AB上的一点,∠BOC=40°,
∴∠AOC=180°-40°=140°,
∵OD、OE分别是∠BOC、∠AOC的角平分线,
∴∠AOE=∠COE=
∠AOC=70°,∠BOD=∠COD=
∠BOC=20°,
∴∠EOC+∠BOD=90°,∠EOC+∠COD=90°,
∴图中与∠EOC互余的角是∠BOD和∠COD;
(2)∠AOE═∠COE=
∠AOC=70°.
∴∠AOC=180°-40°=140°,
∵OD、OE分别是∠BOC、∠AOC的角平分线,
∴∠AOE=∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOC+∠BOD=90°,∠EOC+∠COD=90°,
∴图中与∠EOC互余的角是∠BOD和∠COD;
(2)∠AOE═∠COE=
| 1 |
| 2 |
点评:本题考查了互余,互补的定义的应用,注意:∠A的余角为90°-∠A,∠A的补角是180°-∠A.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
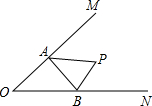 如图,已知∠MON=60°,P为∠MON内一点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数为( )度.
如图,已知∠MON=60°,P为∠MON内一点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数为( )度.| A、40 | B、60 |
| C、100 | D、120 |
已知a-b=5,ab=3,则a2+b2的值是( )
| A、25 | B、28 | C、30 | D、31 |
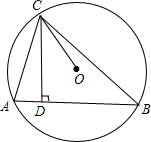 如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.
如图所示,自⊙O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.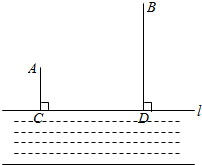 如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为
如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为 如图,已知∠α.
如图,已知∠α. 如图,线段AB上两点C、D,AB=30cm,AC=10cm,BD=5cm,点P从A出发以每秒1cm的速度,沿A→C→D→B→D运动,点Q从B出发,沿B→D→C→A→C运动,P,Q两点运动到终点D,C后停止运动,当Q到达D点时,PA=
如图,线段AB上两点C、D,AB=30cm,AC=10cm,BD=5cm,点P从A出发以每秒1cm的速度,沿A→C→D→B→D运动,点Q从B出发,沿B→D→C→A→C运动,P,Q两点运动到终点D,C后停止运动,当Q到达D点时,PA=