题目内容
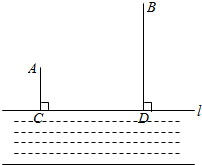如图，已知A，B两个村庄在河流CD的同侧，它们到河流的距离AC=10km，BD=30km，且CD=30km．现在要在河流CD上建立一个泵站P向村庄供水，铺设管道的费用为每千米2万元，要使所花费用最少，请确定泵站P的位置？（保留痕迹，不写作法）此时所花费用最少为考点：轴对称-最短路线问题
专题：
分析：根据已知得出作点A关于直线l的对称点A′，连接A′B，则A′B与直线l的交点P到A、B两点的距离和最小，再利用构造直角三角形得出即可．
解答：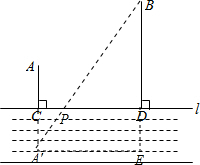
解：依题意，只要在直线l上找一点P，使点P到A、B两点的距离和最小．
作点A关于直线l的对称点A′，连接A′B，
则A′B与直线l的交点P到A、B两点的距离和最小，且PA+PB=PA′+PB=A′B．
过点A′向BD作垂线，交BD的延长线于点E，
在直角三角形A′BE 中，A′E=CD=30，BE=BD+DE=40，
根据勾股定理可得：A′B=50（千米）
即铺设水管长度的最小值为50千米．
所以铺设水管所需费用的最小值为：50×2=100（万元）．
故答案为100万元．
解：依题意，只要在直线l上找一点P，使点P到A、B两点的距离和最小．作点A关于直线l的对称点A′，连接A′B，
则A′B与直线l的交点P到A、B两点的距离和最小，且PA+PB=PA′+PB=A′B．
过点A′向BD作垂线，交BD的延长线于点E，
在直角三角形A′BE 中，A′E=CD=30，BE=BD+DE=40，
根据勾股定理可得：A′B=50（千米）
即铺设水管长度的最小值为50千米．
所以铺设水管所需费用的最小值为：50×2=100（万元）．
故答案为100万元．
点评：此题主要考查了轴对称-最短路线问题和勾股定理的应用，解题关键是构建直角三角形．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
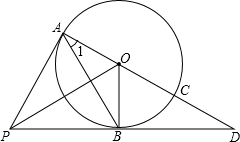如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，AC、PB的延长线相较于点D．
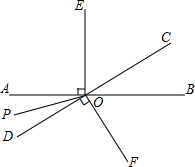如图，直线AB与CD相交于点O，OP是∠AOD的平分线，OE⊥AB，OF⊥CD．
如图，已知点O是直线AB上的一点，∠BOC=40°，OD、OE分别是∠BOC、∠AOC
数学活动课上，老师在黑板上画直线l平行于射线AN（如图），让同学们在直线L和射线AN上各找一点B和C，使得以A、B、C为顶点的三角形是等腰直角三角形．这样的三角形最多能画（ ）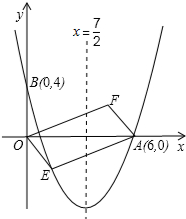
如图，对称轴为直线x=
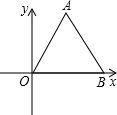如图，△AOB是边长为6的等边三角形，则OA所在直线方程为