题目内容
8.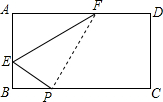 如图,在矩形ABCD中,AB=3,AD=5,E、F分别为边AB、AD上的点,现将△AEF沿直线EF折叠,使得点A恰好落在BC边上的点P处.
如图,在矩形ABCD中,AB=3,AD=5,E、F分别为边AB、AD上的点,现将△AEF沿直线EF折叠,使得点A恰好落在BC边上的点P处.(1)当BP=2时,△EBP的周长=5;
(2)设BP=x,则x的取值范围是1≤x≤3.
分析 (1)根据翻折变换的性质得到EP=AE,根据三角形周长公式求出△EBP的周长;
(2)分点F与D重合和点E与点B重合两种情况求出x的最大值和最小值即可.
解答 解:(1)当BP=2时,设BP=x,则EP=AE=3-x,
由勾股定理得(3-x)2=x2+22,
解得x=$\frac{5}{6}$,
3-x=$\frac{13}{6}$,
则△EBP的周长=5;
(2)当点F与D重合时,FP=AD=5,FC=3,
由勾股定理得PC=4,
则BP=1,
当点E与点B重合时,BP=AB=3,
则1≤x≤3.
故答案为:(1)5;(2)1≤x≤3.
点评 本题考查了翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
18.观察下列前三个式子:$\sqrt{{3}^{2}-1}$=$\sqrt{2}$×$\sqrt{4}$,$\sqrt{{4}^{2}-1}$=$\sqrt{3}$×$\sqrt{5}$,$\sqrt{{5}^{2}-1}$=$\sqrt{4}$×$\sqrt{6}$,…,按照这样的规律第10个式子的结果是( )
| A. | $\sqrt{9}$×$\sqrt{11}$ | B. | $\sqrt{10}$×$\sqrt{12}$ | C. | $\sqrt{11}$×$\sqrt{13}$ | D. | $\sqrt{12}$×$\sqrt{14}$ |
19.已知菱形的周长是16,一边上的高是6,则菱形的面积是( )
| A. | 12 | B. | 24 | C. | 48 | D. | 64 |
13.已知一次函数y=kx+b的图象与直线y=-x+1平行,且过点(1,-2),那么此一次函数的解析式为( )
| A. | y=-x+1 | B. | y=x-1 | C. | y=x+2 | D. | y=-x-1 |
 如图,点H为△ABC的三条高线的交点,点D在△BCH的外接圆上,且AD⊥BD于点D,延长AD交HC于点P,交外接圆于点E.求证:点P为CH的中点.
如图,点H为△ABC的三条高线的交点,点D在△BCH的外接圆上,且AD⊥BD于点D,延长AD交HC于点P,交外接圆于点E.求证:点P为CH的中点.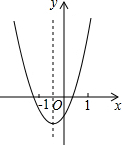 二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )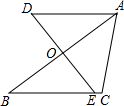 如图,在△ABC中,点O为AB的中点,AD∥BC,过点O的直线交AD,BC于点D,E.求证:OD=OE.
如图,在△ABC中,点O为AB的中点,AD∥BC,过点O的直线交AD,BC于点D,E.求证:OD=OE.