题目内容
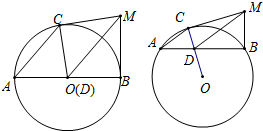
已知AB是⊙O的直径,过B作AB的垂线BM,MC与⊙O相切于C,OC交AB于D,如图1.
(1)求证:AC∥DM;
(2)若AB为⊙O的弦,其他条件不变,求证:AC∥DM.
(1)求证:AC∥DM;
(2)若AB为⊙O的弦,其他条件不变,求证:AC∥DM.

考点:切线的性质
专题:证明题
分析:(1)连接BC,证明M、C、D、B四点共圆;运用切线的性质及圆内接四边形的性质,即可解决问题.
(2)运用同(1)中的思路、方法即可解决问题.
(2)运用同(1)中的思路、方法即可解决问题.
解答: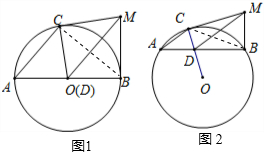 解:(1)如图1,连接BC;
解:(1)如图1,连接BC;
∵BM⊥AB,MC为⊙O的切线,
∴∠MBO+∠MCO=90°+90°=180°,
∴M、C、D、B四点共圆,
∴∠MCB=∠MDB;
又∵MC为⊙O的切线,
∴∠MCB=∠A,
∴∠A=∠MDB,
∴AC∥DM.
(2)如图2,连接BC;
∵BM⊥AB,MC为⊙O的切线,
∴∠MBO+∠MCO=90°+90°=180°,
∴M、C、D、B四点共圆,
∴∠MCB=∠MDB;
又∵MC为⊙O的切线,
∴∠MCB=∠A,
∴∠A=∠MDB,
∴AC∥DM.
 解:(1)如图1,连接BC;
解:(1)如图1,连接BC;∵BM⊥AB,MC为⊙O的切线,
∴∠MBO+∠MCO=90°+90°=180°,
∴M、C、D、B四点共圆,
∴∠MCB=∠MDB;
又∵MC为⊙O的切线,
∴∠MCB=∠A,
∴∠A=∠MDB,
∴AC∥DM.
(2)如图2,连接BC;
∵BM⊥AB,MC为⊙O的切线,
∴∠MBO+∠MCO=90°+90°=180°,
∴M、C、D、B四点共圆,
∴∠MCB=∠MDB;
又∵MC为⊙O的切线,
∴∠MCB=∠A,
∴∠A=∠MDB,
∴AC∥DM.
点评:该命题在考查切线的性质定理的同时,还渗透了对圆内接四边形的判定及其应用的考查;解题的关键是作辅助线,沟通角与角之间的关系,灵活运用切线的性质定理来解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程中,是关于x的一元二次方程的是( )
A、
| ||||
| B、ax2+bx+c=0 | ||||
| C、3x(x-1)+6x=3x2+7 | ||||
| D、5x2=4 |
 如图,AB是圆O的直径,C是圆O上一点,∠ABC的平分线交圆O于E,交AC于D,过E作AC的平行线,交BA的延长线于F.试探索AE,CD,EF线段的关系.
如图,AB是圆O的直径,C是圆O上一点,∠ABC的平分线交圆O于E,交AC于D,过E作AC的平行线,交BA的延长线于F.试探索AE,CD,EF线段的关系.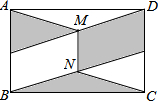 如图,在矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3,BC=2
如图,在矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3,BC=2 如图,数轴上点A表示2,点B表示
如图,数轴上点A表示2,点B表示