题目内容
某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CB的长度也为30 cm,依据是( )
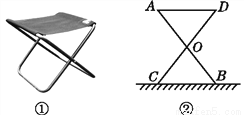
A. SAS B. ASA C. SSS D. AAS
A
【解析】试题解析：∵O是AB、CD的中点，
∴OA=OB，OC=OD，
在△AOD和△BOC中，
，
∴△AOD≌△BOC（SAS），
∴CB=AD，
∵AD=30cm，
∴CB=30cm．
故选A.
（8分）如图所示是由几个小立方体所组成几何体的俯视图，小正方形中的数字表示在该位置的小立方体的个数.
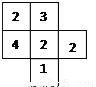
(1)请画出这个几何体的主视图、左视图。
(2)若小立方体的棱长为2cm，求该几何体的表面积。
（1）见解析；（2）184
【解析】试题分析：（1）从正面看有三列，左侧有4行，中间有3行，右侧有2行；从左面看有三列，左侧有3行，中间有4行，右侧有1行；（2）用一个正方形的面积4乘以漏出的小正方形面的个数46即可.
【解析】
（1）如图，
（2）4×（9×2+8×2×+6×2）=184cm2. 如图，图中用数字标出的角中，_____________是同位角，_____________是内错角，_____________是同旁内角；
∠1和∠2 ∠1和∠4 ∠1和∠3
【解析】∠1和∠2是同位角，∠1和∠4是内错角，∠1和∠3是同旁内角； 如图，△ABC中，∠BAC=100°，DF，EG分别是AB，AC的垂直平分线，则∠DAE等于（ ）
A. 50° B. 45° C. 30° D. 20°
D
【解析】试题解析：根据线段的垂直平分线性质，可得AD=BD，AE=CE．
故∠EAC=∠ECA，∠ABD=∠BAD．
因为∠BAC=100°，∠ABD+∠ACE=180°-100°=80°，
∴∠DAE=100°-∠BAD-∠EAC=20°．
故选D. 如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
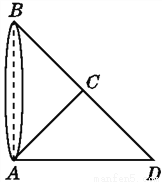
证明见解析.
【解析】试题分析：根据SAS即可证明△ACB≌△ACD，由此即可解决问题．
试题解析：因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD. 如图，已知AE=DB，BC=EF，AC=DF，求证：（1）AC∥DF；（2）CB∥EF．
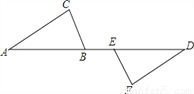
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由SSS证明△ABC≌△DEF，得出对应角相等∠A=∠D，∠ABC=∠DEF，由内错角相等即可得出结论；
（2）由（1）得：∠ABC=∠DEF，得出∠CBE=∠FEB，由内错角相等即可得出结论．
试题解析：（1）∵AE=DB，
∴AE-BE=DB-BE，
即AB=DE，
在△ABC和△DEF中，
，... 如图，AB=AC，BD=CD，则△ABD≌△ACD的依据是（ ）
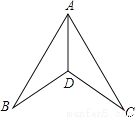
A. SSS B. SAS C. AAS D. HL
A
【解析】在△ABD和△ACD中，
，
∴△ABD和△ACD（SSS）；
故选：A. 下列说法正确的有( )
①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;
③面积相等的两个图形全等;
④周长相等的两个图形全等.
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①两个图形全等，它们的形状相同，故正确；
②两个图形全等，它们的大小相同，故正确；
③面积相等的两个图形全等，错误；
④周长相等的两个图形全等，错误.
故选：B. 若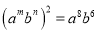
，那么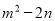
的值是 ( )
A. 10 B. 52 C. 20 D. 32
A
【解析】∵，
∴2m=8,2n=6，
即m=4，n=3，
∴=16-6=10.
故选A.