题目内容

1．若不等式组$\left\{\begin{array}{l}{2x+1＞5}\\{x-m＜0}\end{array}\right.$的正整数解只有三个，则m的取值范围是5＜m≤6．

分析 首先解不等式组，根据不等式组只有三个正整数解，即可确定m的范围．

解答 解：$\left\{\begin{array}{l}{2x+1＞5…①}\\{x-m＜0…②}\end{array}\right.$，
解①得x＞2，
解②得：x＜m．
则不等式组的解集是：2＜x＜m．
则正整数解是3，4，5．
则m的范围是：5＜m≤6．
故答案是：5＜m≤6．

点评 本题考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案
相关题目
11．（1）计算：|-$\sqrt{9}$|+$\root{3}{-8}$-$\sqrt{\frac{1}{4}}$．
（2）解方程组：$\left\{\begin{array}{l}{3x-y-6=0}\\{5y-3x=6}\end{array}\right.$．
12．计算
（1）（-$\sqrt{3}$）2+|3-$\sqrt{12}$|-$\frac{6}{\sqrt{3}}$
（2）已知：x=1-$\sqrt{2}$，y=1+$\sqrt{2}$，求x2+y2-xy-2x+2y的值．
9．一组数据2，4，x，2，4，7的众数是2，则这组数据的平均数、中位数分别为3.5，3．
16．有下列说法：
（1）对顶角相等；
（2）过一点有且只有一条直线与已知直线垂直；
（3）直线外一点到这条直线的垂线段，叫做点到直线的距离；
（4）过一点有且只有一条直线与已知直线平行．
其中正确的说法的个数是（　　）
A．1B．2C．3D．4
6．自2010年4月1日起，新修订的《机动车驾驶证申领和使用规定》正式实施了．新规定为保障公民的人身安全，对被查酒后驾驶机动车（血液酒精含量超过20毫克/百毫升）的驾驶员加大了处罚力度．某交警大队于4月4日～4月10日这7天共查到12起酒后驾车事件，这12位驾车者血液酒精含量（单位：毫克/百毫升）如下：26，58，29，92，21，43，24，27，36，46，23，31．
（1）请计算这些数据的平均数与极差；
（2）请你运用所学到的统计知识估计新规定实施之后一年内（按365天计算），该交警大队能查到多少起酒后驾车事件？（精确到1起）
（3）该交警大队在新规定实施前的某一周7天内共查到38名司机血液酒精含量超过20毫克/百毫升，平均含量为56毫克/百毫升，请结合相关数据谈谈你的想法．
13．化简：$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+ab}$=$\frac{a-b}{a}$，$\frac{1}{m+2}$+$\frac{4}{{m}^{2}-4}$=$\frac{1}{m-2}$．
10．△ABC 中，∠A=90°，a，b，c分别是∠A，∠B，∠C的对边，若a=4，b=3，则c=$\sqrt{7}$．
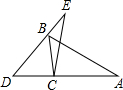11．如图，在△ABC中，∠A：∠ABC：∠ACB=3：5：10，若△EDC≌△ABC，则∠BCE：∠BCD=1：4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网