题目内容
14.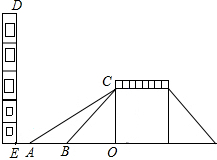 如图是某一过街天桥的示意图,天桥高CO为6米,坡道倾斜角∠CBO为45°,在距B点5米处有一建筑物DE.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角A处之间地面要留出不少于3米宽的人行道.
如图是某一过街天桥的示意图,天桥高CO为6米,坡道倾斜角∠CBO为45°,在距B点5米处有一建筑物DE.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角A处之间地面要留出不少于3米宽的人行道.(1)若将倾斜角改建为30°(即∠CAO=30°),则建筑物DE是否要拆除?( $\sqrt{3}$≈1.732)
(2)若不拆除建筑物DE,则倾斜角最小能改到多少度(精确到1°)?
分析 (1)分别在△CAO和△CBO中,求出AO、BO的长度,最后比较AO+3与OE的长度,进行判断;
(2)若不拆除建筑物DE,则OA最长可以是11-3=8m,在Rt△CAO中,求出∠CAO的度数.
解答 解:(1)当∠CAO=30°时,
在Rt△CAO中,
∵CO=6m,tan∠CAO=$\frac{CO}{AO}$,
∴AO=$\frac{CO}{tan∠CAO}$=$\frac{6}{tan30°}$=6$\sqrt{3}$(m),
在Rt△CBO中,
∵∠CBO=45°,
∴BO=CO=6m,
∵AO+3=6$\sqrt{3}$+3>11=OE,因此建筑物DE要拆除;
(2)若不拆除建筑物DE,则OA最长可以是11-3=8m,
在Rt△CAO中,
∵CO=6m,tan∠CAO=$\frac{CO}{AO}$=$\frac{6}{8}$=0.75,
∴∠CAO≈37°,
因此倾斜角最小能改到37°.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题意构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
6.用“△”表示一种运算符号,其意义是a△b=2a-b,若x△(-1)=2,则x等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
3.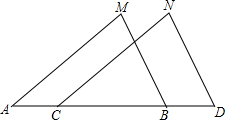 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AC=BD | C. | ∠M=∠N | D. | AM∥CN |
4.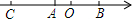 如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )
如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )
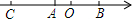 如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )
如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )| A. | -1-$\sqrt{3}$ | B. | -2+$\sqrt{3}$ | C. | -2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
 如图,直线AB、CD相交于点O,OE⊥CD,若∠1=60°,则∠2=30°.
如图,直线AB、CD相交于点O,OE⊥CD,若∠1=60°,则∠2=30°.