题目内容
6.已知:抛物线经过A(0,1),B(1,2),C(-1,-4)三点,求:(1)求抛物线的解析式;
(2)抛物线的开口向上、对称轴是直线x=$\frac{3}{4}$、顶点坐标是($\frac{3}{4}$,$\frac{17}{8}$).
分析 (1)设一般式y=ax2+bx+c,然后把A、B、C三点坐标代入得到关于a、b、c的方程组,然后解方程组即可;
(2)先把(1)中的解析式配成顶点式,然后利用二次函数的性质求解.
解答 解:(1)设抛物线解析式为y=ax2+bx+c,
根据题意得$\left\{\begin{array}{l}{c=1}\\{a+b+c=2}\\{a-b+c=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{b=3}\\{c=1}\end{array}\right.$,
所以抛物线解析式为y=-2x2+3x+1;
(2)y=-2x2+3x+1=-2(x-$\frac{3}{4}$)2+$\frac{17}{8}$,
所以抛物线的开口向上,对称轴是直线x=$\frac{3}{4}$,顶点坐标是($\frac{3}{4}$,$\frac{17}{8}$).
故答案为上,x=$\frac{3}{4}$,($\frac{3}{4}$,$\frac{17}{8}$).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
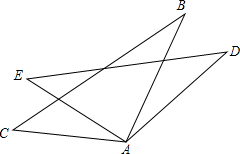 如图,△ABC≌△ADE,点B的对应点是D点,若∠CAD=140°,∠BAE=82°,求∠BAC的度数.
如图,△ABC≌△ADE,点B的对应点是D点,若∠CAD=140°,∠BAE=82°,求∠BAC的度数. 如图,已知0D⊥AB,PO⊥AC,且OD=OP,求证:AO平分∠DAC.
如图,已知0D⊥AB,PO⊥AC,且OD=OP,求证:AO平分∠DAC.