题目内容
18. 若A(m,y1),B(m+2,y2)是如图所示抛物线上的两点,当m取何值时,则①y1=y2?②y1>y2?
若A(m,y1),B(m+2,y2)是如图所示抛物线上的两点,当m取何值时,则①y1=y2?②y1>y2?
分析 由图象可知函数顶点坐标且过点(1,0),可求得抛物线解析式,再分别把A、B点的坐标代入可用m表示出y1和y2,再分别求解即可.
解答 解:
由图象可知函数顶点坐标为(-1,4),且过点(1,0),
∴可设抛物线解析式为y=a(x+1)2+4,
把点(1,0)代入可得4a+4=0,解得a=-1,
∴抛物线解析式为y=-(x+1)2+4=-x2-2x+3,
∵A(m,y1),B(m+2,y2)是抛物线上的两点,
∴y1=-m2-2m+3,y2=-(m+2)2-2(m+2)+3=-m2-6m-5,
①当y1=y2时,则有-m2-2m+3=-m2-6m-5,解得m=-2,
即当m=-2时,y1=y2,
②当y1>y2时,则有-m2-2m+3>-m2-6m-5,即-4m<8,
解得m>-2,
即当m>-2时有y1>y2.
点评 本题主要考查二次函数图象上点的坐标特征,求得二次函数的解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知a为实数,且0<a<1,则a,$\frac{1}{a}$,$\sqrt{a}$,a2中最大的数是( )
| A. | a | B. | $\frac{1}{a}$ | C. | $\sqrt{a}$ | D. | a2 |
6.在△ABC中,点D、E在AB,AC上,给出下列四组条件:
①∠ADE=∠C
②AD•AB=AE•AC
③AD=4,AB=6,DE=2,BC=3
④AD:AB=1:3,AE:EC=1:2
从其中任选一组条件,能判定△ABC和△ADE相似的有( )
①∠ADE=∠C
②AD•AB=AE•AC
③AD=4,AB=6,DE=2,BC=3
④AD:AB=1:3,AE:EC=1:2
从其中任选一组条件,能判定△ABC和△ADE相似的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.若等腰直角三角形的内切圆半径的长为1,则其外接圆半径的长为( )
| A. | $\sqrt{3}+1$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{2}$ | D. | $\sqrt{2}-1$ |
 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0)、B(6,0)两点,且与y轴交于点C(0,2).
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0)、B(6,0)两点,且与y轴交于点C(0,2).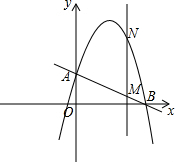 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.