Question

4．等腰三角形的两边长为10和12，则周长为32或34，底边长的高是8或$\sqrt{119}$，面积是48或5$\sqrt{119}$．

Answer 1

分析 需要分类讨论：确定腰和底边的长度，然后再求底边上的高及面积．

解答 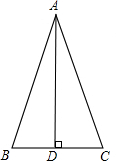解：①当AB=AC=10时，BC=12，则周长=10+10+12=32．
∵等腰△ABC，AD⊥BC，
∴BD=CD=6，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，即高为8．
∴S_△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×12×8=48．
②当AB=AC=12时，BC=10，则周长=10+12+12=34．
∵等腰△ABC，AD⊥BC，
∴BD=CD=5，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{2}^{2}-{5}^{2}}$=$\sqrt{119}$，即高为$\sqrt{119}$．
∴S_△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×10×$\sqrt{119}$=5$\sqrt{119}$．
故答案是：32或34；8或$\sqrt{119}$；48或5$\sqrt{119}$．

点评 本题主要考查等腰三角形的性质、勾股定理、三角形三边关系，关键在于根据有关性质确定等腰三角形的腰长和底边长．