题目内容
14.已知关于x的一元二次方程x2-(2m+1)x+4(m-$\frac{1}{2}$)=0.(1)判断这个一元二次方程的根的情况;
(2)对任意实数m,这个一元二次方程都有一个相同的解,求这个解;
(3)若等腰三角形的一边长为2.5,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长.
分析 (1)先求出△的值,再判断出其符号即可;
(2)对任意实数m,这个一元二次方程都有一个相同的解,得到△=0,求出m=$\frac{3}{2}$,得到方程的根;
(3)分两种情况讨论:若腰=2.5,则x=2.5是方程的一个根,可求得等腰三角形的三边为2.5,2.5,2,那么这个等腰三角形的周长即可求.若底为2.5,则△=0,得到m=$\frac{3}{2}$,可求得等腰三角形的三边为2,2,2.5.那么这个等腰三角形的周长及面积即可求.
解答 解:(1)∵△=(2m+1)2-4×4(m-$\frac{1}{2}$)=(2m-3)2≥0,
∴方程有两个的实数根;
(2)∵对任意实数m,这个一元二次方程都有一个相同的解,
∴△=0,
∴m=$\frac{3}{2}$,
∴方程为;x2-4x+4=0,
∴x1=x2=2;
(3)若腰=2.5,则x=2.5是方程的一个根,
∴另一根为x2=2,
∴等腰三角形的三边为2.5,2.5,2,
∴等腰三角形的周长=7,
若底为2.5,则△=0,得到m=$\frac{3}{2}$,
∴方程的根为:x=2,
∴等腰三角形的三边为2,2,2.5.
∴等腰三角形的周长=6.5.
点评 本题考查的是根的判别式,等腰三角形的性质,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△的关系是解答此题的关键.

练习册系列答案
相关题目
1.为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
| 居民(户) | 1 | 2 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 中位数是50 | B. | 众数是51 | C. | 方差是42 | D. | 极差是21 |
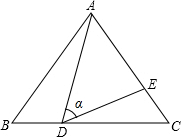 如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且$cosa=\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且$cosa=\frac{4}{5}$.下列结论:
 如图,在钝角△ABC中,BC=9,AB=17,AC=10,AD⊥BC于D,求AD的长.
如图,在钝角△ABC中,BC=9,AB=17,AC=10,AD⊥BC于D,求AD的长. 如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边上的中点,E是AB边上一动点,当EC+ED取最小值时,求△ECB的面积.
如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边上的中点,E是AB边上一动点,当EC+ED取最小值时,求△ECB的面积.