题目内容
8.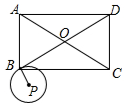 矩形ABCD中,AB=6,BC=6$\sqrt{3}$,半径为$\sqrt{3}$的⊙P与线段BD相切于点M,圆心P与点C在直线BD的同侧,⊙P沿线段BD从点B向点D滚动. 若⊙P与矩形ABCD的两条对角线都相切,则tan∠PBM=$\frac{\sqrt{3}}{5}$或$\frac{\sqrt{3}}{9}$.
矩形ABCD中,AB=6,BC=6$\sqrt{3}$,半径为$\sqrt{3}$的⊙P与线段BD相切于点M,圆心P与点C在直线BD的同侧,⊙P沿线段BD从点B向点D滚动. 若⊙P与矩形ABCD的两条对角线都相切,则tan∠PBM=$\frac{\sqrt{3}}{5}$或$\frac{\sqrt{3}}{9}$.
分析 分两种情形:当点P在△BOC内时,根据切线的性质得到∠BOP=60°,求得BM=5,于是得到tan∠PBM=$\frac{\sqrt{3}}{5}$,当点P在△DOC内时,根据切线的性质得到∠DOP=30°,于是得到tan∠PBM=$\frac{\sqrt{3}}{9}$;
解答 解:当点P在△BOC内时
∵⊙P与AC、BD相切,
∴∠BOP=60°,
∴OM=1,
∴BM=5,
此时tan∠PBM=$\frac{\sqrt{3}}{5}$,
如图4,当点P在△DOC内时,
∵⊙P与AC、BD相切,
∴∠DOP=30°,
∴OM=3,
∴BM=9,
此时tan∠PBM=$\frac{\sqrt{3}}{9}$,
故答案为$\frac{\sqrt{3}}{5}$或$\frac{\sqrt{3}}{9}$.
点评 本题考查了矩形的性质,切线的性质,勾股定理,等边三角形的判定和性质,解直角三角形,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
18.下列每组数表示三根小木棒的长度,三根小棒能摆成三角形的一组是( )
| A. | 1 cm,2 cm,3 cm | B. | 2 cm,3 cm,4 cm | C. | 2 cm,3 cm,5 cm | D. | 2 cm,3 cm,6 cm |
19.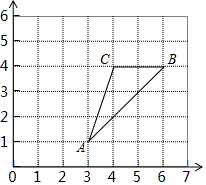 如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
 如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )| A. | (5,1) | B. | (1,1) | C. | (7,1) | D. | (3,3) |
16.若关式方程于x的分式$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$无解,则m的值为( )
| A. | -$\frac{3}{2}$ | B. | 1 | C. | $\frac{3}{2}$或2 | D. | -$\frac{1}{2}$或-$\frac{3}{2}$ |
13.若x2-2x-1=0,则代数式2x2-4x+5的值为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 11 |
17.下列计算正确的是( )
| A. | 4a-3a=1 | B. | a6÷a3=a2 | C. | 2a2•a=2a3 | D. | 3a+2b=5ab |
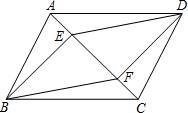 如图,E、F是?ABCD对角线AC上两点,且AE=CF.
如图,E、F是?ABCD对角线AC上两点,且AE=CF.