题目内容
16.若关式方程于x的分式$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$无解,则m的值为( )| A. | -$\frac{3}{2}$ | B. | 1 | C. | $\frac{3}{2}$或2 | D. | -$\frac{1}{2}$或-$\frac{3}{2}$ |
分析 根据分式方程的解法即可求出答案.
解答 解:x(2m+x)-x(x-3)=2(x-3)
2mx+x2-x2+3x=2x-6
2mx+x=-6
当2m+1≠0时,
∴x=$\frac{-6}{2m+1}$,
∵该分式方程无解,
∴将x=$\frac{-6}{2m+1}$代入x(x-3)=0,
∴$\frac{-6}{2m+1}$($\frac{-6}{2m+1}$-3)=0,
∴解得:m=-$\frac{3}{2}$
当2m+1=0时,
∴m=-$\frac{1}{2}$,此时分式方程无解,符合题意,
故选(D)
点评 本题考查分式方程的解法,解题的关键是熟练运用分式方程的解法,本题属于基础题型.

练习册系列答案
相关题目
6.一次知识竞赛共有20道选择题,规定答对一道得5,不做或做错一题扣1分,如果某学生做对题数为x,用代数式表示他的得分为( )
| A. | 5x-(20-x) | B. | 100-(20-x) | C. | 5x | D. | 5x-5(20-x)-(20-x) |
7.若a>b,则下列不等式中错误的是( )
| A. | -$\frac{a}{7}$<-$\frac{b}{7}$ | B. | -(-a)>-(-b) | C. | a-2>b-2 | D. | -2a+1>-2b+1 |
4.下列说法正确的是( )
| A. | 0的算术平方根是0 | B. | 9是3的算术平方根 | ||
| C. | ±3是9的算术平方根 | D. | -3是9的算术平方根 |
1.$\frac{1}{4}$的相反数为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
 如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为2cm.
如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为2cm.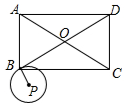 矩形ABCD中,AB=6,BC=6$\sqrt{3}$,半径为$\sqrt{3}$的⊙P与线段BD相切于点M,圆心P与点C在直线BD的同侧,⊙P沿线段BD从点B向点D滚动. 若⊙P与矩形ABCD的两条对角线都相切,则tan∠PBM=$\frac{\sqrt{3}}{5}$或$\frac{\sqrt{3}}{9}$.
矩形ABCD中,AB=6,BC=6$\sqrt{3}$,半径为$\sqrt{3}$的⊙P与线段BD相切于点M,圆心P与点C在直线BD的同侧,⊙P沿线段BD从点B向点D滚动. 若⊙P与矩形ABCD的两条对角线都相切,则tan∠PBM=$\frac{\sqrt{3}}{5}$或$\frac{\sqrt{3}}{9}$.