题目内容
抛物线y=x2-3x与x轴的交点坐标为 .
考点:抛物线与x轴的交点
专题:
分析:要求抛物线与x轴的交点,即令y=0,解方程即可.
解答:解:令y=0,则x2-3x=0.
解得x=3或x=0.
则抛物线y=x2-3x与x轴的交点坐标是(3,0),(0,0).
故答案为(3,0),(0,0).
解得x=3或x=0.
则抛物线y=x2-3x与x轴的交点坐标是(3,0),(0,0).
故答案为(3,0),(0,0).
点评:本题考查了抛物线与x轴的交点.求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
在同一平面内,连接一个定点和圆上的任意一点的线段中,最短为4cm,最长为9cm,则该圆的半径是( )
| A、2.5cm或6.5cm |
| B、2.5cm |
| C、6.5cm |
| D、5cm或13cm |
在-25,0,
,2.5这四个数中,绝对值最大的数是( )
| 2 |
| 5 |
| A、-25 | ||
| B、0 | ||
C、
| ||
| D、2.5 |
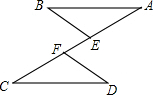 如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是
如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是 长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.
长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.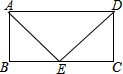 如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为
如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为