题目内容
7．
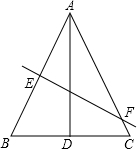如图，△ABC中，AB=AC，BC=5，S△ABC=15，AD⊥BC与点D，EF垂直平分AB，交AC于F，在EF上确定一点P使PB+PD最小，则这个最小值为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 根据三角形的面积公式得到AD=6，由EF垂直平分AB，得到点A，B关于执行EF对称，于是得到AD的长度=PB+PD的最小值，即可得到结论．
解答 解：∵AB=AC，BC=5，S△ABC=15，AD⊥BC与点D，
∴AD=6，
∵EF垂直平分AB，
∴点A，B关于执行EF对称，
∴AD的长度=PB+PD的最小值，
即PB+PD的最小值为6，
故选D．
点评 本题考查了轴对称-最短路线问题，线段的垂直平分线的性质，等腰三角形的性质，知道AD的长度=PB+PD的最小值是解题的关键．
练习册系列答案
相关题目
18．自从隧道扫描显微镜发明后，世界上便诞生了一门新学科，这就是“纳米技术”．已知52纳米的长度为0.000000052米．将0.000000052用科学记数法表示为（ ）
| A． | 5.2×10-8 | B． | 52×10-9 | C． | 0.52×10-7 | D． | 5.2×10-7 |
2．
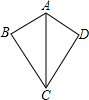如图，∠BAC=∠DAC，若添加一个条件仍不能判断出△ABC≌△ADC的是（ ）
如图，∠BAC=∠DAC，若添加一个条件仍不能判断出△ABC≌△ADC的是（ ）| A． | AB=AD | B． | BC=DC | C． | ∠B=∠D | D． | ∠ACB=∠ACD |
19．以下列各组线段长为边能组成三角形的是（ ）
| A． | 1cm 2cm 4cm | B． | 8cm 6cm 4cm | C． | 12cm 5cm 6cm | D． | 2cm 3cm 6cm |
16．下列命题是真命题的是（ ）
| A． | 有且只有一条直线垂直于已知直线 | |
| B． | 从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离 | |
| C． | 直线b外一点A与直线b上各点连接而成的所有线段中，最短线段的长是5cm，则点A到直线b的距离是5cm | |
| D． | 同旁内角互补 |