题目内容
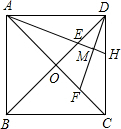 如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.(1)求证:①AE=DF;②AM⊥DF;
(2)若M为DF中点,连接EF,直接写出
| EF |
| DC |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)①根据DE=CF,可得出OE=OF,继而证明△AOE≌△DOF,得出AE=DF,②由△AOE≌△DOF得出∠OAE=∠ODF,然后利用等角代换可得出∠DME=90°,得出了结论.
(2)连结EF,利用△EMD≌△EMF,求出线段之间的关系求解.
(2)连结EF,利用△EMD≌△EMF,求出线段之间的关系求解.
解答:(1)证明:①∵四边形ABCD是正方形,
∴CO=DO,
又∵DE=CF,
∴OD-DE=OC-CF,即OF=OE,
在△AOE和△DOF中,
,
∴△AOE≌△DOF(SAS),
∴AE=DF,
②由①中△AOE≌△DOF,
∴∠OAE=∠ODF,
∵∠OAE+∠AEO=90°,∠AEO=∠DEM,
∴∠ODF+∠DEM=90°,
即可得AM⊥DF;
(2)如图连接EF
由AM⊥DF,M为DF中点,
∴
∴△EMD≌△EMF(SAS),
∴EF=ED,
∵四边形ABCD是正方形,
∴∠DOB=90°,∠OCD=45°,
∴DC=
OD=
(OE+ED),
∵OE=
EF,
∴DC=
(
EF+EF),
∴DC=EF(1+
),
∴
=
-1,
故答案为:
-1.
∴CO=DO,
又∵DE=CF,
∴OD-DE=OC-CF,即OF=OE,
在△AOE和△DOF中,
|
∴△AOE≌△DOF(SAS),
∴AE=DF,
②由①中△AOE≌△DOF,
∴∠OAE=∠ODF,
∵∠OAE+∠AEO=90°,∠AEO=∠DEM,
∴∠ODF+∠DEM=90°,
即可得AM⊥DF;
(2)如图连接EF

由AM⊥DF,M为DF中点,
∴
|
∴△EMD≌△EMF(SAS),
∴EF=ED,
∵四边形ABCD是正方形,
∴∠DOB=90°,∠OCD=45°,
∴DC=
| 2 |
| 2 |
∵OE=
| ||
| 2 |
∴DC=
| 2 |
| ||
| 2 |
∴DC=EF(1+
| 2 |
∴
| EF |
| DC |
| 2 |
故答案为:
| 2 |
点评:此题考查了正方形的性质、全等三角形的判定与性质,解答本题的关键是通过全等的证明和利用等角代换解题.

练习册系列答案
相关题目

 如图,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的圆交x轴于D、E两点(点D在点E的右方),求点E、D的坐标.
如图,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的圆交x轴于D、E两点(点D在点E的右方),求点E、D的坐标. 已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)
已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)