题目内容
9.已知y=y1-y2,且y1与x2成正比例,y2与x-2成正比例,且当x=1时,y=0;当x=-3时,y=4.(1)求y与x之间的函数关系式;
(2)当x=3时,求y的值.
分析 (1)设y1=kx2,y2=d(x-2),则y=y1-y2=kx2-d(x-2)=kx2-dx+2d,将x=1时,y=0;x=-3,y=4分别代入解析式即可得到k,d的值;
(2)将x=3代入y=x2+x-2即可解答.
解答 解:(1)设y1=kx2,y2=d(x-2),
则y=y1-y2=kx2-d(x-2)=kx2-dx+2d,
当x=1时,y=0;当x=-3时,y=4,
可知$\left\{\begin{array}{l}k-d+2d=0\\ 9k+3d+2d=4\end{array}\right.$,
整理得$\left\{\begin{array}{l}k+d=0\\ 9k+5d=4\end{array}\right.$,
解得$\left\{\begin{array}{l}k=1\\ d=-1\end{array}\right.$.
故函数解析式为y=x2+x-2.
(2)当x=3时,y=9+3-2=10.
点评 本题考查了待定系数法求二次函数解析式,熟悉正比例函数的定义,根据题意得到方程组是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
7.下列计算正确的是( )
| A. | a8÷a4=a2 | B. | x2+x3=x5 | C. | (-c3)•(-c)5=c8 | D. | (-x-y)(-x+y)=-x2+y2 |
 如图,在△ABC中,AB=AC=3,∠BAC=120°,以点A为圆心,1为半径作圆弧,分别交AB,AC于点D,E,以点C为圆心,3为半径作圆弧,分别交AC,BC于点A,F.若图中阴影部分的面积分别为S1,S2,则S1-S2的值为$\frac{9\sqrt{3}}{4}$-$\frac{47}{6}$π.
如图,在△ABC中,AB=AC=3,∠BAC=120°,以点A为圆心,1为半径作圆弧,分别交AB,AC于点D,E,以点C为圆心,3为半径作圆弧,分别交AC,BC于点A,F.若图中阴影部分的面积分别为S1,S2,则S1-S2的值为$\frac{9\sqrt{3}}{4}$-$\frac{47}{6}$π.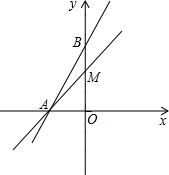 如图,在平面直角坐标系中,函数y=2x+4的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.
如图,在平面直角坐标系中,函数y=2x+4的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.