题目内容
20.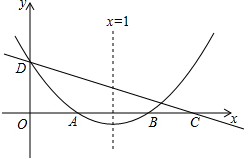 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )①abc>0; ②3a+b>0; ③-1<k<0; ④4a+2b+c<0; ⑤a+b<k.
| A. | ①②③ | B. | ②③⑤ | C. | ②④⑤ | D. | ②③④⑤ |
分析 由抛物线的开口判断a的符号;由对称轴判断b及b与2a的关系;由抛物线与y轴的交点判断c的符号;由抛物线和直线图象上点的坐标判断有关代数式的符号.
解答 解:∵抛物线开口向上,
∴a>0.
∵抛物线对称轴是x=1,
∴b<0且b=-2a.
∵抛物线与y轴交于正半轴,
∴c>0.
∴①abc>0错误;
∵b=-2a,
∴3a+b=3a-2a=a>0,
∴②3a+b>0正确;
∵b=-2a,
∴4a+2b+c=4a-4a+c=c>0,
∴④4a+2b+c<0错误;
∵直线y=kx+c经过一、二、四象限,
∴k<0.
∵OA=OD,
∴点A的坐标为(c,0).
直线y=kx+c当x=c时,y>0,
∴kc+c>0可得k>-1.
∴③-1<k<0正确;
∵直线y=kx+c与抛物线y=ax2+bx+c的图象有两个交点,
∴ax2+bx+c=kx+c,
得x1=0,x2=$\frac{k-b}{a}$.
由图象知x2>1,
∴$\frac{k-b}{a}$>1
∴k>a+b,
∴⑤a+b<k正确,
即正确命题的是②③⑤.
故选B.
点评 本题考查的是二次函数图象与系数的关系和一次函数的性质以及抛物线与直线的交点的求法,掌握一、二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
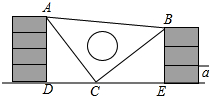 课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.