题目内容
19.如果(x+1)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,试求:a1+a3+a5.分析 根据二项展开式的通项公式展开可得a1+a3+a5.=C${\;}_{6}^{1}$+C${\;}_{6}^{3}$+C${\;}_{6}^{5}$,计算求出结果.
解答 解:a1+a3+a5.=C${\;}_{6}^{1}$+C${\;}_{6}^{3}$+C${\;}_{6}^{5}$=32.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式某项的系数,属于中档题目.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
12.已知一次函数y=$\frac{3}{2}$x+a与y=-$\frac{1}{2}$x+b的图象都经过点A(-2,0),且与y轴分别交于B,C两点,那么△ABC的面积是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.计算:(-3)+5的结果是( )
| A. | -2 | B. | 2 | C. | 8 | D. | -8 |
7.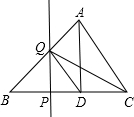 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )| A. | $\frac{9}{5}$或4 | B. | $\frac{6}{5}$或4 | C. | $\frac{9}{5}$或$\frac{13}{5}$ | D. | $\frac{6}{5}$或$\frac{13}{5}$ |
4. 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |
9.金秋十月,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如表:
(1)如果他批发80千克太湖蟹,则他在A 家批发需要4416元,在B家批发需要4380元;
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
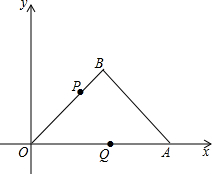 如图,∠OAB=45°,点A的坐标是(4,0),AB=$2\sqrt{2}$,连结OB.
如图,∠OAB=45°,点A的坐标是(4,0),AB=$2\sqrt{2}$,连结OB.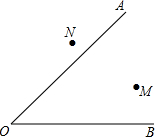 已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).
已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).