题目内容
12.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53$\frac{3}{7}$,问删去的那个数是多少?分析 基于平均数的考虑:1,2,3,4,…,105的平均数是53,1,2,3,4,…,106的平均数是53.5,它应该有105个或106个连续数,由于减去一个数的平均为53$\frac{3}{7}$,当n=105个,但104×53$\frac{3}{7}$不是整数,故否定了有105个数.当106个数时,可以尝试错误法找出.
解答 解:1,2,3,4,….,105的平均数是53,
1,2,3,4,….,106的平均数是53.5
它应该有105个或106个连续数.
(1)由于减去一个数的平均为53$\frac{3}{7}$,当n=105个,但104×53$\frac{3}{7}$不是整数,故否定了有105个数.
(2)当106个数时,很明显不会删去106,故应是1-105中其中一个数,考虑平均数的分数部,由于是105个数的平均,故将$\frac{3}{7}$=$\frac{45}{105}$,当中表示删去的数为106-45=61,或1+2+3+…+106=5671,
当减去一个数后,平均为53$\frac{3}{7}$,n=105,
和=53$\frac{3}{7}$×105=5610,
所以减去的一个数应是5671-5610=61.
答:删去的那个数是61.
点评 本题考查的是样本平均数的求法及运用,解题的关键是先确定连续自然数介于105个或106个连续数,然后讨论即可.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.下列计算正确的是( )
| A. | (x3)3=x9 | B. | (-2x)3=-6x3 | C. | 2x2-x=x | D. | x2÷x3=x2 |
20.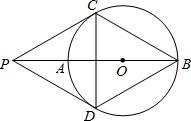 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.等腰三角形的底边长10cm,周长36cm,则底角的余弦值为( )
| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
 如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4.
如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4. 如图,一张纸上有A、B、C、D四个点,请找出一点M,使得MA=MB,MC=MD.
如图,一张纸上有A、B、C、D四个点,请找出一点M,使得MA=MB,MC=MD.