题目内容
14.如图,已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.(1)点C的坐标是(4,3);
(2)以线段AD的中点M为圆心作⊙M,当⊙M与直线CE相切时,求⊙M的半径;
(3)如图2,点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q两点同时出发,速度均为1单位长度/s,时间为t s.当p、q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2.

分析 (1)首先求出点D的坐标是多少,进而确定出线段CD所在的直线的解析式;然后联立CD所在的直线的解析式:y=$\frac{3}{4}$x,求出点C的坐标是多少即可;
(2)首先求出线段AD的中点M的坐标;然后根据点到直线的距离的求法,求出点M到直线y=$\frac{3}{4}$x的距离,即可判断出⊙M的半径是多少;
(3)先得出直线BC的解析式,设点M的坐标为(x,1.5x-3),同时得出点P和点Q的坐标,根据两点间的距离公式得出PQ=PM,继而得出答案.
解答 解:(1)∵y=3x+3与y轴的交点D的坐标是(0,3),
∴线段CD所在的直线的解析式是:y=3,
联立$\left\{\begin{array}{l}{y=3}\\{y=\frac{3}{4}x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
即点C的坐标是(4,3);
(2)由0=3x+3,
解得x=-1,
∴点A的坐标是(-1,0),
∴线段AD的中点M的坐标是(-$\frac{1}{2}$,$\frac{3}{2}$),
由y=$\frac{3}{4}$x,可得
3x-4y=0,
当⊙M与直线CE相切时,⊙M的半径是:
$\frac{|3×(-\frac{1}{2})-4×\frac{3}{2}|}{\sqrt{{3}^{2}{+(-4)}^{2}}}$
=$\frac{7.5}{5}$
=1.5
(3)如图2,点Q落在四边形ABCD的BC边所在的直线上, ,
,
设直线BC的解析式为:y=kx+b,
把点C(4,3)和点B(2,0)代入可得:
$\left\{\begin{array}{l}{3=4k+b}\\{0=2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1.5}\\{b=-3}\end{array}\right.$,
所以解析式为:y=1.5x-3,
设点M的坐标为(x,1.5x-3),
因为直线OC过原点和点C(4,3),可得直线OC的解析式为:y1=$\frac{4}{3}$x;
当点Q落在四边形ABCD一边所在的直线上时,点P的坐标为($\frac{3}{5}t,\frac{4}{5}t$),点Q的坐标为(3-t,4),
将线段PQ绕点P沿顺时针方向旋转90°,可得PQ=PM,
可得:$(\frac{3}{5}t-3+t)^{2}+(\frac{4}{5}t-4)^{2}=(\frac{3}{5}t-x)^{2}+(\frac{4}{5}t-1.5x+3)^{2}$,$2[(\frac{3}{5}t-3+t)^{2}+(\frac{4}{5}t-4)^{2}]=(3-t-x)^{2}+(4-1.5x+3)^{2}$,
联立两个方程解得:t=2.
故答案为:2.
点评 此题主要考查了一次函数综合题,考查了分析推理能力,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.同时还考查了点的坐标的求法,以及直线的解析式的求法,还有直线和圆相切的性质的应用,要熟练掌握.

 高中必刷题系列答案
高中必刷题系列答案| A. | (x3)3=x9 | B. | (-2x)3=-6x3 | C. | 2x2-x=x | D. | x2÷x3=x2 |

 已知:如图,△ABC中,AB=AC,BD是AC边上的高
已知:如图,△ABC中,AB=AC,BD是AC边上的高 如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4.
如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4. 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC. 如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC=4.
如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC=4.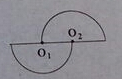 如图,⊙O1、⊙O2分别是两个半圆的圆心,这个圆形是中心对称图形吗?如果是,请指出对称中心;如果不是,请说明理由.
如图,⊙O1、⊙O2分别是两个半圆的圆心,这个圆形是中心对称图形吗?如果是,请指出对称中心;如果不是,请说明理由.