题目内容
如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB=
r(r是⊙O的半径).
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)如图2,当F是AB的四等分点且EF•EC=
r2时,求EC的值.
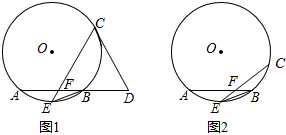
| 2 |
| 3 |
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)如图2,当F是AB的四等分点且EF•EC=
| 4 |
| 9 |
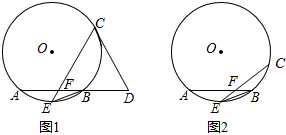
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)连接OC,OE,利用垂径定理结合已知条件求出∠OCD=90°即可;
(2)连接OA,设OH=x,表示出HE,分别在Rt△OAH和Rt△EHA中利用勾股定理可解出x,再结合F是四等分点和已知关系可求出EC的值.
(2)连接OA,设OH=x,表示出HE,分别在Rt△OAH和Rt△EHA中利用勾股定理可解出x,再结合F是四等分点和已知关系可求出EC的值.
解答:(1)证明:连结OC、OE,OE交AB于H,如图1,
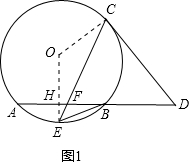
∵E是弧AB的中点,
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
而∠HFE=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
而OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)解:如图2,连接OA,
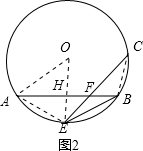
∵
=
,
∴AE=BE=
r,
设OH=x,则HE=r-x,
在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,
在Rt△EAH中,AH2+EH2=EA2,即AH2+(r-x)2=(
r)2,
∴x2-(r-x)2=r2-(
r)2,解得x=
r,
∴HE=r-
r=
r,
在Rt△OAH中,AH=
=
=
,
∵OE⊥AB,
∴AH=BH,
而F是AB的四等分点,
∴HF=
AH=
,
在Rt△EFH中,EF=
=
=
r,
∵EF•EC=
r2,
∴EC=
r.

∵E是弧AB的中点,
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
而∠HFE=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
而OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)解:如图2,连接OA,

∵
 |
| AE |
 |
| BE |
∴AE=BE=
| 2 |
| 3 |
设OH=x,则HE=r-x,
在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,
在Rt△EAH中,AH2+EH2=EA2,即AH2+(r-x)2=(
| 2 |
| 3 |
∴x2-(r-x)2=r2-(
| 2 |
| 3 |
| 7 |
| 9 |
∴HE=r-
| 7 |
| 9 |
| 2 |
| 9 |
在Rt△OAH中,AH=
| OA2-OH2 |
r2-(
|
4
| ||
| 9 |
∵OE⊥AB,
∴AH=BH,
而F是AB的四等分点,
∴HF=
| 1 |
| 2 |
2
| ||
| 9 |
在Rt△EFH中,EF=
| HE2+HF2 |
(
|
2
| ||
| 9 |
∵EF•EC=
| 4 |
| 9 |
∴EC=
2
| ||
| 3 |
点评:本题主要考查切线的判定及垂径定理,在(1)中掌握切线的判定方法是解题的关键,在(2)中求出HF的值是解题的关键.

练习册系列答案
相关题目
响水县实验初中的校园面积约是102000平方米,用科学记数法表示为( )
| A、102×103 |
| B、10.2×104 |
| C、1.02×105 |
| D、0.102×106 |
n边形的每个外角都为36°,则边数n为( )
| A、10 | B、14 | C、15 | D、16 |
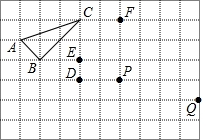 如图,在正方形格纸中,△ABC的三个顶点及D、E、F、P、Q五个点分别位于边长为1的小正方形的顶点上,先从P、Q两个点中任意取一个点,再从D、E、F三个点中任意取两个点,以所取的这三个点为顶点组成三角形,求所组成的三角形与△ABC相似的概率(用画树状图或列表法求解).
如图,在正方形格纸中,△ABC的三个顶点及D、E、F、P、Q五个点分别位于边长为1的小正方形的顶点上,先从P、Q两个点中任意取一个点,再从D、E、F三个点中任意取两个点,以所取的这三个点为顶点组成三角形,求所组成的三角形与△ABC相似的概率(用画树状图或列表法求解).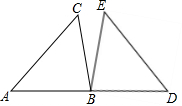 在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.
在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积. 如图,在⊙O中,AB⊥OC,垂足为D,AD=3,OD=4,该圆的直径为
如图,在⊙O中,AB⊥OC,垂足为D,AD=3,OD=4,该圆的直径为