题目内容
【题目】等腰△BCD中,∠DCB=120°,点E满足∠DEC=60°.
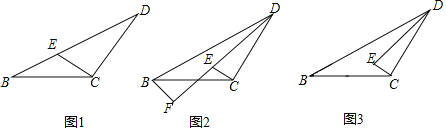
(1)如图1,点E在边BD上时,求证:ED=2BE;
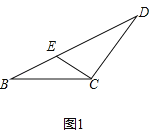
(2)如图2,过点B作DE的垂线交DE的延长线于点F,试探究DE和EF的数量关系,并证明;
(3)若∠DEB=150°,直接写出BE,DE和EC的关系.
【答案】(1)见解析;(2)DE=2EF.理由见解析;(3)BE2=EDEC.理由见解析.
【解析】
(1)先根据等腰三角形性质和三角形外角的性质得:BC=CD和BE=CE,根据三角形的内角和定理证明∠DCE=180°-30°-60°=90°,由直角三角形30度角的性质可得结论.
(2)结论:DE=2EF.如图2中,作DH⊥EC交EC的延长线于H,连接FH.想办法证明DE=2EH,EF=EH即可解决问题.
(3)结论:BE2=EDEC.证明△DEB∽△BEC可得结论.
(1)证明:如图1中,
∵等腰△BCD中,∠DCB=120°,
∴BC=CD,
∴∠B=∠D=30°,
∵∠DEC=60°=∠B+∠ECB,
∴∠ECB=30°,
∴BE=CE,
△DEC中,∠DCE=180°﹣30°﹣60°=90°,
∵∠D=30°,
∴ED=2EC,
∴ED=2BE;
(2)解:结论:DE=2EF.
理由:如图2中,作DH⊥EC交EC的延长线于H,连接FH.

∵∠DHE=90°,∠DEH=60°,
∴∠EDH=30°,
∵CD=CB,∠BCD=120°,
∴∠CBD=∠BDC=30°,
∴∠BDC=∠EDH,
∴∠BDF=∠CDH,
∵BF⊥DF,
∴∠BFD=∠H=90°,
∴△DFB∽△DHC,
∴![]() ,
,
∴![]() ,
,
∵∠BDC=∠FDH,
∴△BDC∽△FDH,
∴∠DBC=∠DFH=30°,
∵∠DEH=∠EFH+∠EHF=60°,
∴∠EFH=∠EHF=30°,
∴EF=EH,
在Rt△DEH中,∵∠EDH=30°,
∴DE=2EFH,
∴DE=2EF.
(3)解:结论:BE2=EDEC.
理由:如图3中,
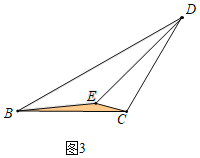
∵∠BED=150°,∠DEC=60°,
∴∠BEC=360°∠BED﹣∠DEC=360°﹣150°﹣60°=150°,
∴∠BED=∠BEC,
∴∠EBD+∠EDB=30°,
∵∠EBD+∠EBC=30°,
∴∠BDE=∠EBC,
∴△DEB∽△BEC,
∴![]() ,
,
∴BE2=DEEC.

 阅读快车系列答案
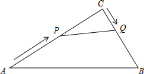
阅读快车系列答案【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() .(若同学们打印的BC的长度如不是
.(若同学们打印的BC的长度如不是![]() ,请同学们重新画图、测量)
,请同学们重新画图、测量)
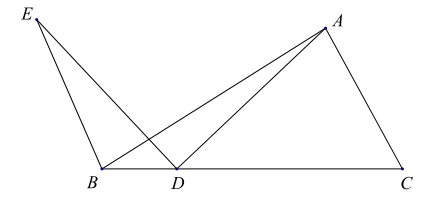
小明根据学习函数的经验,分别对![]() 自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出![]() 的值.(保留1位小数)
的值.(保留1位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
(3)结合函数图像,解决问题:
①当![]() 在线段
在线段![]() 上时,
上时,![]() 的长度约为________
的长度约为________![]() ;
;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度
的长度![]() 约为_______
约为_______![]() .
.