题目内容
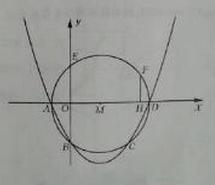
如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.
(1)当AB=2时,求△GEC的面积;
(2)求证:AE=EF.
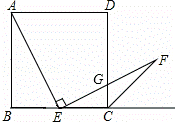
解:(1)∵AB=BC=2,点E为BC的中点,
∴BE=EC=1,
∵AE⊥EF,
∴△ABE∽△ECG,
∴AB:EC=BE:GC,
即:2:1=1:GC,
解得:GC= ,
,
∴S△GEC= •EC•CG=
•EC•CG= ×1×
×1× =
= ;
;
(2)证明:取AB的中点H,连接EH;
∵ABCD是正方形,
AE⊥EF;
∴∠1+∠AEB=90°,
∠2+∠AEB=90°
∴∠1=∠2,
∵BH=BE,∠BHE=45°,
且∠FCG=45°,
∴∠AHE=∠ECF=135°,AH=CE,
∴△AHE≌△ECF,
∴AE=EF;


练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 有意义,则x的取值范围是
有意义,则x的取值范围是 
 的自变量x的取值范围是
的自变量x的取值范围是 
 C. ﹣3 D.
C. ﹣3 D. 
 与⊙M相交于A、B、C、D四点。其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点。其中AB两点的坐标分别为(-1,0),(0,-2),点D在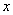 轴上且AD为⊙M的直径。点E是⊙M与
轴上且AD为⊙M的直径。点E是⊙M与 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧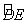 上的点F作FH⊥AD于点H,且FH=1.5。
上的点F作FH⊥AD于点H,且FH=1.5。