题目内容
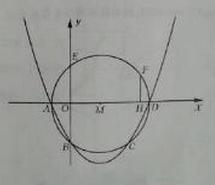
如图,在平面直角坐标系中,抛物线 与⊙M相交于A、B、C、D四点。其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点。其中AB两点的坐标分别为(-1,0),(0,-2),点D在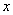 轴上且AD为⊙M的直径。点E是⊙M与
轴上且AD为⊙M的直径。点E是⊙M与 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧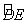 上的点F作FH⊥AD于点H,且FH=1.5。
上的点F作FH⊥AD于点H,且FH=1.5。
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是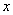 轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由。
 |
第(1)问求抛物线的解析式,我们知道的条件就是AB两点的坐标,要想求得抛物线的解析式,必须再有一个点才行。根据题意,设点M的坐标为(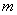 ,0),根据两点间的距离公式(半径相等)可以求得
,0),根据两点间的距离公式(半径相等)可以求得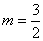 ,则点D的坐标为(4,0),这样就可以根据交点式来求解抛物线的解析式:
,则点D的坐标为(4,0),这样就可以根据交点式来求解抛物线的解析式: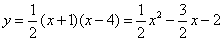
第(2)问其实是我们初中阶段经常练习的一个轴对称问题。要在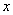 轴上的找到一点P,使得⊿PEF的周长最小,我们先来看E,F两点,这是两个定点,也就是说EF的长度是不变的,那实际上这个题目就是求PE+PF的最小值,这就变成了轴对称问题中最为经典的“放羊问题”,要解决这一问题首先我们看图中有没有E或F的对称点,根据题意,显然是有E点的对称点B的,那么连接BF与
轴上的找到一点P,使得⊿PEF的周长最小,我们先来看E,F两点,这是两个定点,也就是说EF的长度是不变的,那实际上这个题目就是求PE+PF的最小值,这就变成了轴对称问题中最为经典的“放羊问题”,要解决这一问题首先我们看图中有没有E或F的对称点,根据题意,显然是有E点的对称点B的,那么连接BF与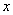 轴的交点就是我们要求的点P(2,0)。
轴的交点就是我们要求的点P(2,0)。
第(3)问要在抛物线的对称轴上找点Q,使得⊿QCM是等腰三角形,首先点M本身就在抛物线对称轴上,其坐标为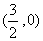 ;点C是点B关于抛物线对称轴的对称点,所以点C的坐标为(3,-2);求Q点的坐标,根据题意可设Q点为(
;点C是点B关于抛物线对称轴的对称点,所以点C的坐标为(3,-2);求Q点的坐标,根据题意可设Q点为( )。⊿QCM是等腰三角形,则可能有三种情况,分别是QC=MC;QM=MC;QC=QM。根据这三种情况就能求得Q点的坐标可能是
)。⊿QCM是等腰三角形,则可能有三种情况,分别是QC=MC;QM=MC;QC=QM。根据这三种情况就能求得Q点的坐标可能是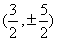 或
或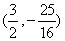 或
或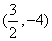

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 B.
B. 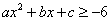
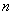 ) 在抛物线上,则
) 在抛物线上,则
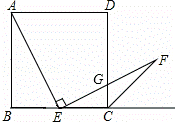
 的两根为-5和-1
的两根为-5和-1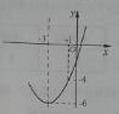
 ,再从
,再从 的范围内选取一个你喜欢的
的范围内选取一个你喜欢的 x2
x2 ﹣(m﹣1)x+3,当x<﹣3时,y随x的增大而减小”成为随机事件.
﹣(m﹣1)x+3,当x<﹣3时,y随x的增大而减小”成为随机事件. 时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).